题目内容
过点P（2，1）引一条直线，使它与点A（3，2）和点B（5，-4）的距离相等，那么这条直线的方程是（ ）
| A．x+y-3=0或3x+y-7=0 | B．x-y-3=0或x+3y-7=0 |
| C．x+y-3=0 | D．3x+y-7=0 |
当直线与AB平行时，由于kAB=
=-3，
∴过点P（2，1）的直线方程为y-1=-3（x-2），即3x+y-7=0；
当直线与AB相交时，由于AB中点为（4，-1），
∴过点P（2，1）的直线方程为
=
，即x+y-3=0．
∴过点P（2，1），与点A（3，2）和点B（5，-4）的距离相等的直线的方程是x+y-3=0或3x+y-7=0．
故选：A．
| -4-2 |
| 5-3 |
∴过点P（2，1）的直线方程为y-1=-3（x-2），即3x+y-7=0；
当直线与AB相交时，由于AB中点为（4，-1），
∴过点P（2，1）的直线方程为
| y+1 |
| 1+1 |
| x-4 |
| 2-4 |
∴过点P（2，1），与点A（3，2）和点B（5，-4）的距离相等的直线的方程是x+y-3=0或3x+y-7=0．
故选：A．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
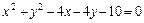上的点到直线
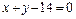的最大距离与最小距离的差是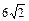
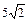
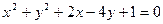关于直线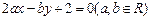
对称，则ab的取值范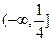
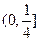
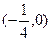
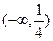
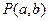
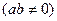是圆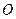
：
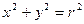内一点，直线
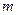是以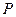
为中点的弦所在的直线，若直线
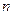的方程为
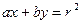，则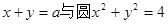
交于A、B两点，O是坐标原点，向量
、
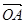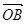满足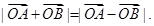
，则实数a的值是 （ ）
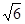或－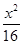
－
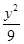＝1的两条渐近线都相切的圆的方程为________．