题目内容
已知直线l1：3x-4y-12=0与l2：ax+8y-11=0平行，则l1与l2的距离为______．
∵直线l1：3x-4y-12=0与l2：ax+8y-11=0平行，
∴
=
≠
，解之得a=-6
因此直线l2方程为-6x+8y-11=0，再将l1化成-6x+8y+24=0
由平行两条直线之间的距离，得l1与l2的距离为
d=
=
故答案为：
∴
| a |
| 3 |
| 8 |
| -4 |
| -11 |
| -12 |
因此直线l2方程为-6x+8y-11=0，再将l1化成-6x+8y+24=0
由平行两条直线之间的距离，得l1与l2的距离为
d=
| |-11-24| | ||
|
| 7 |
| 2 |
故答案为：
| 7 |
| 2 |
练习册系列答案
名校课堂系列答案
相关题目
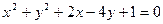关于直线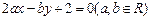
对称，则ab的取值范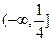
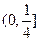
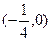
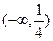
）关于直线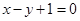
对称，并且圆C与
－
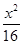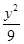＝1的两条渐近线都相切的圆的方程为________．
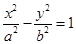的一个焦点为
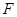，以坐标原点
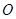为圆心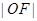
为半径的圆与双曲线的一条渐近线的一个交点为
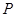，若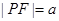
，则双曲线的离心率为 .