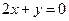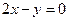题目内容
(本小题满分16分)
已知⊙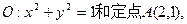 由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足
由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足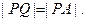 (1)求实数a,b间满足的等量关系;(2)求线段PQ长的最小值;
(1)求实数a,b间满足的等量关系;(2)求线段PQ长的最小值;
(3)若以P为圆心所作的⊙P与⊙O有公共点,试求半径最小值时⊙P的方程。
已知⊙
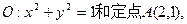 由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足
由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足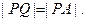 (1)求实数a,b间满足的等量关系;(2)求线段PQ长的最小值;
(1)求实数a,b间满足的等量关系;(2)求线段PQ长的最小值;(3)若以P为圆心所作的⊙P与⊙O有公共点,试求半径最小值时⊙P的方程。
:(Ⅰ)  (Ⅱ)
(Ⅱ) 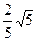 (Ⅲ)
(Ⅲ) 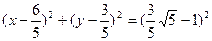
 (Ⅱ)
(Ⅱ) 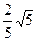 (Ⅲ)
(Ⅲ) 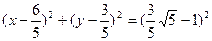
:(1)连OP,
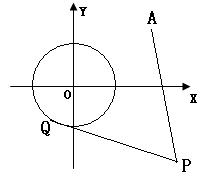
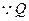 为切点,PQ⊥OQ,由勾股定理有
为切点,PQ⊥OQ,由勾股定理有
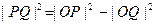
又由已知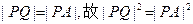
即: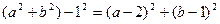
化简得实数a、b间满足的等量关系为:
 ……5分
……5分
(2)由 ,得b=-2a+3 。
,得b=-2a+3 。
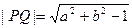
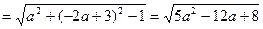
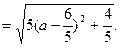
故当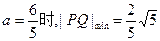 ,即线段PQ长的最小值为
,即线段PQ长的最小值为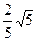 ………………10分
………………10分
(3)设⊙P的半径为R,OP设⊙O有公共点,⊙O的半径为1,
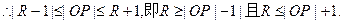
而
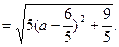
故当
得半径取最小值⊙P的方程为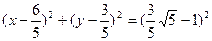 …………………15分
…………………15分
点评:本小题主要考查直线、圆和不等式等基本知识,考查平面解析几何的基本方法,考查运算能力和综合解题能力。
易错点:计算一定要细致,解析几何题的运算过程中的失误是最常见的现象.

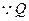 为切点,PQ⊥OQ,由勾股定理有
为切点,PQ⊥OQ,由勾股定理有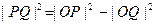
又由已知
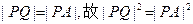
即:
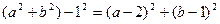
化简得实数a、b间满足的等量关系为:
 ……5分
……5分(2)由
 ,得b=-2a+3 。
,得b=-2a+3 。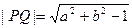
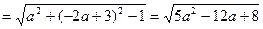
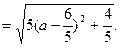
故当
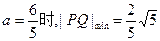 ,即线段PQ长的最小值为
,即线段PQ长的最小值为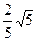 ………………10分
………………10分(3)设⊙P的半径为R,OP设⊙O有公共点,⊙O的半径为1,
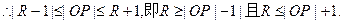
而

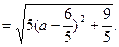
故当

得半径取最小值⊙P的方程为
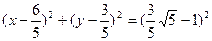 …………………15分
…………………15分点评:本小题主要考查直线、圆和不等式等基本知识,考查平面解析几何的基本方法,考查运算能力和综合解题能力。
易错点:计算一定要细致,解析几何题的运算过程中的失误是最常见的现象.

练习册系列答案
相关题目


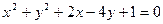 关于直线
关于直线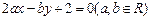 对称,则ab的取值范
对称,则ab的取值范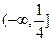
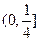
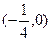
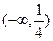
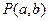
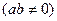 是圆
是圆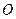 :
: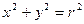 内一点,直线
内一点,直线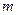 是以
是以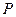 为中点的弦所在的直线,若直线
为中点的弦所在的直线,若直线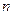 的方程为
的方程为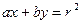 ,则
,则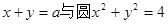 交于A、B两点,O是坐标原点,向量
交于A、B两点,O是坐标原点,向量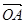 、
、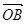 满足
满足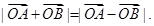 ,则实数a的值是 ( )
,则实数a的值是 ( )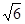 或-
或- )关于直线
)关于直线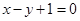 对称,并且圆C与
对称,并且圆C与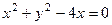 在点
在点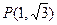 处的切线方程为( )
处的切线方程为( )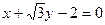
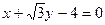
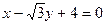
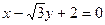
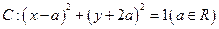 ,则下列一定经过圆心的直线方程为
,则下列一定经过圆心的直线方程为