题目内容
20.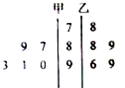 如图是甲、乙两位射击运动员的5次训练成绩(单位:环)的茎叶图,则成绩较为稳定(方差较小)的运动员是甲.
如图是甲、乙两位射击运动员的5次训练成绩(单位:环)的茎叶图,则成绩较为稳定(方差较小)的运动员是甲.
分析 根据茎叶图中的数据,计算甲、乙二人的平均数与方差,即可得出正确的结论.
解答 解:根据茎叶图中的数据,得;
甲的平均数是${\overline{x}}_{甲}$=$\frac{1}{5}$(87+89+90+91+93)=90,
乙的平均数是$\overline{{x}_{乙}}$=$\frac{1}{5}$(78+88+89+96+99)=90,
甲的方差是${{s}_{甲}}^{2}$=$\frac{1}{5}$[(87-90)2+(89-90)2+(90-90)2+(91-90)2+(93-90)2]=4,
乙的方差是${{s}_{乙}}^{2}$=$\frac{1}{5}$[(78-90)2+(88-90)2+(89-90)2+(96-90)2+(99-90)2]=53.2,
∵${{s}_{甲}}^{2}$<${{s}_{乙}}^{2}$,∴成绩较稳定的是甲.
故答案为:甲.
点评 本题考查了利用茎叶图计算(估算)数据的平均数和方差的应用问题,是基础题目.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
11.若$cos(\frac{π}{6}-α)=m,(|m|≤1)$,则$sin(\frac{2π}{3}-α)$的值为( )
| A. | -m | B. | $-\frac{m}{2}$ | C. | $\frac{m}{2}$ | D. | m |
8.某饮料销售点销售某品牌饮料,饮料的零售价x(元/瓶)与销量y(瓶)的关系统计如下:
由表中数据得线性回归方程:$\widehat{y}$=-20x+a,当零售价为每瓶3.7元时,估计该销售点销售的这种饮料的瓶数为( )
| 零售价x(元/瓶) | 3.0 | 3.2 | 3.4 | 3.6 | 3.8 | 4.0 |
| 销量y(瓶) | 50 | 44 | 43 | 40 | 35 | 28 |
| A. | 39 | B. | 38 | C. | 37 | D. | 36 |
12.极坐标方程ρcosθ=2sin2θ表示的曲线为( )
| A. | 一条射线和一个圆 | B. | 一条直线和一个圆 | ||
| C. | 两条直线 | D. | 一个圆 |
3.某工厂为了对新研究的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
(1)求回归直线方程$\hat y=\hat bx+\hat a$,其中$\hat b$=-20.
(2)预计在今后的销售中,销售与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价定为多少元?
| 单价x元 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销售y件 | 90 | 84 | 83 | 80 | 75 | 68 |
(2)预计在今后的销售中,销售与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价定为多少元?