题目内容
9.点(x,y)在直线x+3y-2=0上移动时,z=2x+8y的最小值为4.分析 根据基本不等式的性质进行计算即可.
解答 解:∵x+3y-2=0,∴x+3y=2,
∴z=2x+23y≥2$\sqrt{{2}^{x}{•2}^{3y}}$=2$\sqrt{{2}^{x+3y}}$=2$\sqrt{{2}^{2}}$=4,
当且仅当x=3y,即x=1,y=$\frac{1}{3}$时,“=”成立,
故答案为:4.
点评 本题考查了基本不等式的性质,应用性质是注意满足条件;一正二定三相等,本题是一道基础题.

练习册系列答案
相关题目
17.设m、n为两条不重合的直线,α,β为两个不重合的平面,下列命题中正确的是( )
| A. | 若m、n与α所成的角相等,则m∥n | B. | 若n∥α,m∥β,α∥β,则m∥n | ||
| C. | 若n?α,m?β,m∥n,则α∥β | D. | 若n⊥α,m⊥β,α⊥β,则n⊥m |
14.下列结论正确的是( )
| A. | 若ac>bc,则a>b | B. | 若a2>b2,则a>b | ||
| C. | 若a>b,c>d,则ac>bd | D. | 若a>b>0,则a>$\frac{a+b}{2}>\sqrt{ab}$>b |
12.已知0<a<1<b,则下面不等式中一定成立的是( )
| A. | logab+logba+2>0 | B. | logab+logba+2<0 | C. | logab+logba+2≥0 | D. | logab+logba+2≤0 |
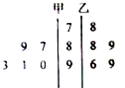 如图是甲、乙两位射击运动员的5次训练成绩(单位:环)的茎叶图,则成绩较为稳定(方差较小)的运动员是甲.
如图是甲、乙两位射击运动员的5次训练成绩(单位:环)的茎叶图,则成绩较为稳定(方差较小)的运动员是甲.