��Ŀ����
3��ij����Ϊ�˶����о���һ�ֲ�Ʒ���к������ۣ����ò�Ʒ�������ⶨ�ļ۸�����������õ��������ݣ�| ����xԪ | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| ����y�� | 90 | 84 | 83 | 80 | 75 | 68 |
��2��Ԥ���ڽ��������У������뵥����Ȼ���ӣ�1���еĹ�ϵ���Ҹò�Ʒ�ijɱ���4Ԫ/����Ϊʹ�������������ò�Ʒ�ĵ��۶�Ϊ����Ԫ��
���� ��1������ƽ����������$\hat b$=-20�����$\widehat{a}$��������ûع�ֱ�߷��̣�
��2���蹤����õ�����ΪyԪ����������=��������-�ɱ������������������䷽��������õ��������
��� �⣺��1��$\overline{x}=\frac{8+8.2+8.4+8.6+8.8+9}{6}=8.5$��
$\overline{y}$=$\frac{1}{6}��90+84+83+80+75+68��=80$
��$\hat b$=-20��$\widehat{a}$=$\overline{y}$-$\hat b$$\overline x$��
��$\widehat{a}$=80+20��8.5=250
��ع�ֱ�߷���$\widehaty$=-20x+250��
��2���蹤����õ�����ΪyԪ����y=x��-20x+250��-4��-20x+250��=-20${��x-\frac{33}{4}��}^{2}+361.25$
��ò�Ʒ�ĵ���Ӧ��Ϊ$\frac{33}{4}$Ԫ��������õ��������
���� ������Ҫ����ع������������κ�������������������Ӧ����ʶ�������е��⣮

��ϰ��ϵ�д�
 ������ÿ�ʱ��ҵϵ�д�
������ÿ�ʱ��ҵϵ�д�
�����Ŀ
5����Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0��������Ϊ$\frac{\sqrt{3}}{2}$����˫��$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1�����߷��̣�������
| A�� | x��2y=0 | B�� | 2x��y=0 | C�� | x��4y=0 | D�� | x��2y=0 |
12����֪0��a��1��b�������治��ʽ��һ���������ǣ�������
| A�� | logab+logba+2��0 | B�� | logab+logba+2��0 | C�� | logab+logba+2��0 | D�� | logab+logba+2��0 |
13��������A={x|x2-2x+m=0}=∅����ʵ��m��ȡֵ��Χ�ǣ�������
| A�� | ��-�ޣ�-1�� | B�� | ��-�ޣ�1�� | C�� | ��1��+�ޣ� | D�� | [1��+�ޣ� |
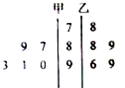 ��ͼ�Ǽס�����λ����˶�Ա��5��ѵ���ɼ�����λ�������ľ�Ҷͼ����ɼ���Ϊ�ȶ��������С�����˶�Ա�Ǽף�
��ͼ�Ǽס�����λ����˶�Ա��5��ѵ���ɼ�����λ�������ľ�Ҷͼ����ɼ���Ϊ�ȶ��������С�����˶�Ա�Ǽף�