题目内容
【题目】在矩形ABCD中,边AB、AD的长分别为2,1,若M,N分别是边BC、CD上的点,且满足 ![]() =
= ![]() =λ.
=λ. 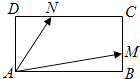
(1)当λ= ![]() 时,求向量
时,求向量 ![]() 和
和 ![]() 夹角的余弦值;
夹角的余弦值;
(2)求 ![]() 的取值范围.
的取值范围.
【答案】
(1)解法一:当 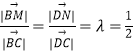 时
时 ![]() ,
,
![]()
![]()
![]()
![]()
![]() BC,CD
BC,CD ![]() )
)
设向量 ![]() 和
和 ![]() 夹角为θ
夹角为θ
则 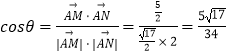 )
)
解法二:以A为原点,分别以AB,AD为x,y轴建立直角坐标系xAy,如图所示:
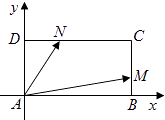
则A(0,0),B(2,0),D(0,1)
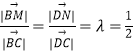 时,
时, ![]() ,
,
![]() ,
, ![]() ,
,
![]()
设向量 ![]() 和
和 ![]() 夹角为θ,则
夹角为θ,则 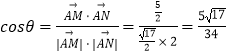
(2)解法一:当 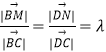 时,因为M,N分别是边上,所以0≤λ≤1.
时,因为M,N分别是边上,所以0≤λ≤1.
![]() ,
, ![]() ,
,
![]() ,
, ![]()
![]() )
)
因为0≤λ≤1
所以 ![]() 的取值范围是[0,5].
的取值范围是[0,5].
解法二:当 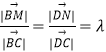 时,因为 M,N分别是边BC,CD上.所以0≤λ≤1
时,因为 M,N分别是边BC,CD上.所以0≤λ≤1
![]()
![]() ,
,
![]() ,
, ![]()
![]()
因为0≤λ≤1,所以 ![]() 的取值范围是[0,5]
的取值范围是[0,5]
【解析】(1)法1:根据向量数量积的公式直接进行求解即.法2:建立坐标系,求出向量坐标,利用向量数量积的坐标公式进行求解.(2)法1:利用三点关系,建立数乘向量关系,结合向量数量积的定义进行求解.法2:利用坐标系,求出向量坐标,利用向量数量积的坐标公式进行求解.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
