题目内容
、(本题满分12分)
定义 的零点
的零点 为
为 的不动点.已知函数
的不动点.已知函数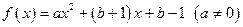
⑴ 当 时,求函数
时,求函数 的不动点;
的不动点;
⑵ 对于任意实数 ,函数
,函数 恒有两个相异的不动点,求
恒有两个相异的不动点,求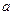
 的取值范围;
的取值范围;
⑶ 若函数 有不变号零点,且
有不变号零点,且 ,求实数
,求实数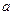 的最小值.
的最小值.
定义
 的零点
的零点 为
为 的不动点.已知函数
的不动点.已知函数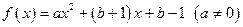
⑴ 当
 时,求函数
时,求函数 的不动点;
的不动点;⑵ 对于任意实数
 ,函数
,函数 恒有两个相异的不动点,求
恒有两个相异的不动点,求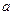
 的取值范围;
的取值范围;⑶ 若函数
 有不变号零点,且
有不变号零点,且 ,求实数
,求实数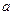 的最小值.
的最小值.(1) -1或3
(2)

(3) 1
解⑴当
 时,
时,  =
=
令


 =-1或
=-1或 =3…………………………1分
=3…………………………1分∴函数
 的不动点为-1或3……………………3分
的不动点为-1或3……………………3分⑵

 =0有两个相异实根
=0有两个相异实根即方程
 有两个相异实根……………………4分
有两个相异实根……………………4分∴△=
 对于任意实数
对于任意实数 成立
成立∴16
 ∴
∴ ……………………6分
……………………6分⑶

 =0有两个相等实根
=0有两个相等实根即方程
 有两个相等实根……………………8分
有两个相等实根……………………8分∴△=

∵
 ∴
∴ ……………………10分
……………………10分令
 ,则
,则 ,且
,且
∴

令

 ,易证函数
,易证函数 在
在 上单调递减,在
上单调递减,在 上单调递增
上单调递增∴
 的最小值为
的最小值为 ="1 " ∴实数
="1 " ∴实数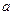 的最小值是1. ……………………12分
的最小值是1. ……………………12分
练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
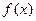 对于其定义域内的某一数
对于其定义域内的某一数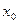 ,有
,有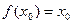 ,则称
,则称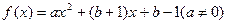 .
.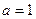 ,
,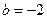 时,求函数
时,求函数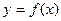
 图象上两个点A、B的横坐标是函数
图象上两个点A、B的横坐标是函数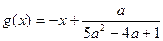 的图象上,求b的最小值.
的图象上,求b的最小值.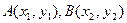 的中点坐标为
的中点坐标为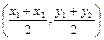 )
)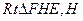 是直角
是直角 顶点)来处理污水,管道越长,污水净化效果越好。设计要求管道的接口H是AB的中点,E、F分别落在线段BC、AD上,已知AB=20米,
顶点)来处理污水,管道越长,污水净化效果越好。设计要求管道的接口H是AB的中点,E、F分别落在线段BC、AD上,已知AB=20米,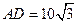 米,记
米,记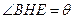 。
。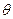 的函数,并写出定义域;
的函数,并写出定义域;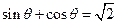 ,求此时管道的长度L;
,求此时管道的长度L;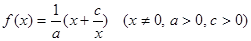 ,当
,当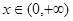 时,函数
时,函数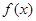 在x=2处取得最小值1。
在x=2处取得最小值1。 的解析式;
的解析式;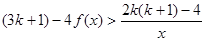 。
。 3分)
3分)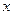 km
km 车运输的总费用分别为
车运输的总费用分别为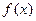 与
与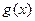 ,求
,求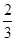 倍,且对每个项目的投资不能低于5万元;对甲项目每投资1万元可获得0.4万元的利润,对乙项目每投资1万元可获得0.6万元的利润,如该公司在正确规划后,在这两个项目上共可获得的最大利润为 万元。
倍,且对每个项目的投资不能低于5万元;对甲项目每投资1万元可获得0.4万元的利润,对乙项目每投资1万元可获得0.6万元的利润,如该公司在正确规划后,在这两个项目上共可获得的最大利润为 万元。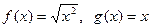
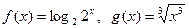
 的方程
的方程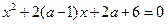 有一正一负两实根,实数
有一正一负两实根,实数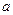 取值范围__
取值范围__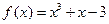 的零点落在区间
的零点落在区间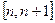
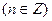 内,则n =" " ▲
内,则n =" " ▲