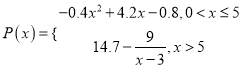题目内容
【题目】已知函数f(x)=ax2+bx和g(x)=lnx. (Ⅰ) 若a=b=1,求证:f(x)的图象在g(x)图象的上方;
(Ⅱ) 若f(x)和g(x)的图象有公共点P,且在点P处的切线相同,求a的取值范围.
【答案】解:(Ⅰ)证明:若a=b=1,即有f(x)=x2+x,
令h(x)=f(x)﹣g(x)=x2+x﹣lnx,h′(x)=2x+1﹣ ![]() =
= ![]()
= ![]() ,x>0,
,x>0,
当x> ![]() 时,h′(x)>0,h(x)递增;当0<x<
时,h′(x)>0,h(x)递增;当0<x< ![]() 时,h′(x)<0,h(x)递减.
时,h′(x)<0,h(x)递减.
可得h(x)在x= ![]() 处取得极小值,且为最小值,且h(
处取得极小值,且为最小值,且h( ![]() )=
)= ![]() +
+ ![]() ﹣ln
﹣ln ![]() >0,
>0,
即有h(x)>0恒成立,则f(x)的图象在g(x)图象的上方;
(Ⅱ)设P的坐标为(m,n),
f(x)=ax2+bx的导数为f′(x)=2ax+b,
g(x)=lnx的导数为g′(x)= ![]() ,
,
可得2am+b= ![]() ,且n=am2+bm=lnm,
,且n=am2+bm=lnm,
消去b,可得am2+1﹣2am2=lnm,
可得a= ![]() (m>0),
(m>0),
令u(m)= ![]() (m>0),
(m>0),
则u′(m)= ![]() ,
,
当m>e ![]() 时,u′(m)>0,u(m)递增;当0<m<e
时,u′(m)>0,u(m)递增;当0<m<e ![]() 时,u′(m)<0,u(m)递减.
时,u′(m)<0,u(m)递减.
可得u(m)在m=e ![]() 处取得极小值,且为最小值,且u(e
处取得极小值,且为最小值,且u(e ![]() )=
)= ![]() =﹣
=﹣ ![]() ,
,
则a≥﹣ ![]() ,
,
故a的取值范围是[﹣ ![]() ,+∞)
,+∞)
【解析】(Ⅰ)令h(x)=f(x)﹣g(x)=x2+x﹣lnx,求出导数和单调区间,可得极小值,且为最小值,判断最小值大于0,即可得证;(Ⅱ)设P的坐标为(m,n),分别求出f(x),g(x)的导数,可得切线的斜率,即有2am+b= ![]() ,且n=am2+bm=lnm,消去b,可得a=
,且n=am2+bm=lnm,消去b,可得a= ![]() (m>0),令u(m)=
(m>0),令u(m)= ![]() (m>0),求出导数和单调区间、极值和最值,即可得到所求范围.
(m>0),求出导数和单调区间、极值和最值,即可得到所求范围.
【考点精析】关于本题考查的函数的最大(小)值与导数,需要了解求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.
比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.

【题目】某数学教师对所任教的两个班级各抽取20名学生进行测试,分数分布如表,若成绩120分以上(含120分)为优秀.
分数区间 | 甲班频率 | 乙班频率 |
[0,30) | 0.1 | 0.2 |
[30,60) | 0.2 | 0.2 |
[60,90) | 0.3 | 0.3 |
[90,120) | 0.2 | 0.2 |
[120,150] | 0.2 | 0.1 |
优秀 | 不优秀 | 总计 | |
甲班 | |||
乙班 | |||
总计 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
(Ⅰ)求从乙班参加测试的90分以上(含90分)的同学中,随机任取2名同学,恰有1人为优秀的概率;
(Ⅱ)根据以上数据完成上面的2×2列联表:在犯错概率小于0.1的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关?