题目内容
已知(
-
)n(n∈N*)的展开式中第五项的系数与第三项的系数的比是10:1.
(1)求展开式中各项系数的和;
(2)求展开式中含x
的项.
| x |
| 2 |
| x2 |
(1)求展开式中各项系数的和;
(2)求展开式中含x
| 3 |
| 2 |
由题意知,展开式的通项为
Tr+1=
(-2)rx
则第五项系数为Cn4•(-2)4,第三项的系数为Cn2•(-2)2
则有
=
,化简,得n2-5n-24=0
解得n=8或n=-3(舍去)
(1)令x=1,得各项系数的和为(1-2)8=1
(2)令
-2r=
,则r=1
故展开式中含x
的项为T2=-16x
Tr+1=
| C | rn |
| n-5r |
| 2 |
则第五项系数为Cn4•(-2)4,第三项的系数为Cn2•(-2)2
则有
16
| ||
4
|
| 10 |
| 1 |
解得n=8或n=-3(舍去)
(1)令x=1,得各项系数的和为(1-2)8=1
(2)令
| 8-r |
| 2 |
| 3 |
| 2 |
故展开式中含x
| 3 |
| 2 |
| 3 |
| 2 |

练习册系列答案
相关题目
 的社长是高中学生,
的社长是高中学生, 的社长是初中学生,高中社长中有
的社长是初中学生,高中社长中有 是高一学生,初中社长中有
是高一学生,初中社长中有 是初二学生.
是初二学生. ,求
,求 .
.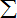
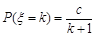 (k=0,1,2,3),则
(k=0,1,2,3),则 .
. 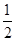 外,其余每局比赛甲队获胜的概率都是
外,其余每局比赛甲队获胜的概率都是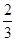 ,假设各局比赛结果相互独立.
,假设各局比赛结果相互独立.