题目内容
已知f（x，y）=（ax+by+1）n（常数a，b∈Z，n∈N*且n≥2）
（1）若a=-2，b=0，n=2010，记f(x，y)=a0+
aixi求：①
ai；②
iai
（2）若f（x，y）展开式中不含x的项的系数的绝对值之和为729，不含y项的系数的绝对值之和为64，求n的所有可能值．
（1）若a=-2，b=0，n=2010，记f(x，y)=a0+
| 2010 |
 |
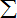| i=1 |
| 2010 |
|
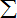| i=1 |
| 2010 |
|
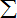| i=1 |
（2）若f（x，y）展开式中不含x的项的系数的绝对值之和为729，不含y项的系数的绝对值之和为64，求n的所有可能值．
（1）由已知，令x=0，得a0=1，l令x=1，得a0+
ai=（-2+1）2010=1，①
ai=0
②f（x，y）=（-2x+1）2010=(2x-1)2010=a0+
aixi两边同时对x求导，得2010（2x-1）2009×2=
iaixi-1，再令x=1得
iai=4020
（2）令a=0得（by+1）n，则（|b|+1）n=729
令b=0，（ax+1）n，则（|a|+1）n=64
因为64所有的底数与指数均为正整数的指数式拆分为：82，43，26
所以当n=2时，|a|=7，|b|=26；当n=3时，|a|=3，|b|=8；当n=6时，|a|=1，|b|=2
故n的所有的可能值为2，3，6
| 2010 |
|
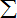| i=1 |
| 2010 |
|
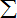| i=1 |
②f（x，y）=（-2x+1）2010=(2x-1)2010=a0+
| 2010 |
|
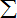| i=1 |
| 2010 |
|
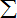| i=1 |
| 2010 |
|
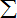| i=1 |
（2）令a=0得（by+1）n，则（|b|+1）n=729
令b=0，（ax+1）n，则（|a|+1）n=64
因为64所有的底数与指数均为正整数的指数式拆分为：82，43，26
所以当n=2时，|a|=7，|b|=26；当n=3时，|a|=3，|b|=8；当n=6时，|a|=1，|b|=2
故n的所有的可能值为2，3，6
练习册系列答案
相关题目
四所中学报名参加某高校今年自主招生的学生人数如下表所示：
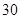
名学生中随机抽取两名学生，求这两名学生自同一所中学的概率；
两所中学的学生当中随机抽取两名学
表示抽得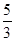
，V(η)＝
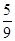，求a∶b∶c.