Question

【题目】设函数.

（1）请作出该函数在长度为一个周期的闭区间的大致图象；

（2）试判断该函数的奇偶性，并运用函数的奇偶性定义说明理由；

（3）求该函数的单调递增区间．

Answer 1

【答案】（1）见解析；（2）见解析；（3）.

【解析】

（1）用五点法作图，作出该函数在长度为一个周期的闭区间的大致图象．（2）利用正弦函数的奇偶性作出判断．（2）利用正弦函数的单调性，求函数单调递增区间．

（1）函数f（x）＝sin2x+cos2x＝sin（2x+），

列表：

2x+	0		π		2π
x	﹣
f（x）	0		0	﹣	0

作图：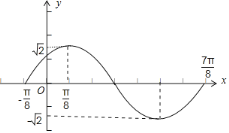

（2）该函数为非奇非偶，

∵f（﹣x）＝sin（﹣2x+），而f（x）＝sin（2x+），

﹣f（x）＝﹣sin（2x+），

∴f（﹣x）≠f（x），且f（x）≠﹣f（x），故f（x）为非奇非偶函数．

（3）令2kπ﹣≤2x+≤2kπ+，求得kπ﹣≤x≤kπ+，

可得它的增区间为