题目内容
10.将函数f(x)=sin(2x-$\frac{π}{6}$)的图象上所有的点向左平移$\frac{π}{3}$个单位(纵坐标不变),则所得图象的解析式是( )| A. | y=-cos2x | B. | y=cos2x | C. | y=sin(2x-$\frac{5π}{6}$) | D. | y=sin(2x+$\frac{π}{6}$) |
分析 由条件利用函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答 解:将函数f(x)=sin(2x-$\frac{π}{6}$)的图象上所有的点向左平移$\frac{π}{3}$个单位,可得y=sin[2(x+$\frac{π}{3}$)-$\frac{π}{6}$]=sin(2x+$\frac{π}{2}$)=cos2x的图象,
故选:B.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.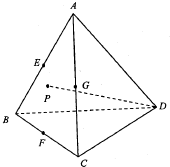 如图E、F、G分别是各棱长均相等的三棱锥A-BCD的棱AB、BC、AC的中点,点P在侧面ABC及其边界上运动,DP⊥AB,则动点P的轨迹是( )
如图E、F、G分别是各棱长均相等的三棱锥A-BCD的棱AB、BC、AC的中点,点P在侧面ABC及其边界上运动,DP⊥AB,则动点P的轨迹是( )
 如图E、F、G分别是各棱长均相等的三棱锥A-BCD的棱AB、BC、AC的中点,点P在侧面ABC及其边界上运动,DP⊥AB,则动点P的轨迹是( )
如图E、F、G分别是各棱长均相等的三棱锥A-BCD的棱AB、BC、AC的中点,点P在侧面ABC及其边界上运动,DP⊥AB,则动点P的轨迹是( )| A. | 线段FG | B. | 线段EG | C. | 线段EF | D. | 线段EC |
5.定积分$\int_0^1{(2x-{e^x})}$dx的值为( )
| A. | 2-e | B. | -e | C. | e | D. | 2+e |
15.16个同类产品中有14个正品,2个次品,从中任意抽取3个,则下列事件中概率为1的是( )
| A. | 三个都是正品 | B. | 三个都是次品 | ||
| C. | 三个中至少有一个是正品 | D. | 三个中至少有一个次品 |
 在一段时间内有100辆汽车经过某交通岗,有2辆汽车速度小于35km/h,有3辆汽车的速度大于75km/h,时速(单位:km/h)频率分布直方图如图所示,
在一段时间内有100辆汽车经过某交通岗,有2辆汽车速度小于35km/h,有3辆汽车的速度大于75km/h,时速(单位:km/h)频率分布直方图如图所示,