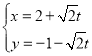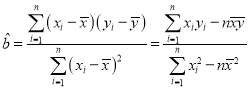题目内容
【题目】设函数![]() .
.
(1)若a=0时,求函数![]() 的单调递增区间;
的单调递增区间;
(2)若函数![]() 在x=1时取极大值,求实数a的取值范围;
在x=1时取极大值,求实数a的取值范围;
(3)设函数![]() 的零点个数为m,试求m的最大值.
的零点个数为m,试求m的最大值.
【答案】(1)单调增区间为(1,)(2)![]() (3)2
(3)2
【解析】
(1)求导得到函数的单调增区间.
(2)求导,讨论![]() ,
,![]() ,
,![]() 或
或![]() ,
,![]() 几种情况,分别计算函数极值得到答案.
几种情况,分别计算函数极值得到答案.
(3)考虑![]() ,
,![]() 两种情况,求导得到单调区间,计算极值判断零点个数,得到答案.
两种情况,求导得到单调区间,计算极值判断零点个数,得到答案.
(1)当a=0时,![]() ,所以
,所以![]() ,由
,由![]() 得x=1,
得x=1,
当x(0,1)时,![]() <0;当x(1,)时,
<0;当x(1,)时,![]() >0,
>0,
所以函数![]() 的单调增区间为(1,).
的单调增区间为(1,).
(2)由题意得![]() ,
,
令![]() (x>0),则
(x>0),则![]() ,
,
当![]() ≥0即
≥0即![]() 时,
时,![]() >0恒成立,
>0恒成立,
故![]() 在(0,1)上递减,在(1,+)上递增,所以x=1是函数
在(0,1)上递减,在(1,+)上递增,所以x=1是函数![]() 的极小值点,不满足;
的极小值点,不满足;
当![]() 即
即![]() 时,此时
时,此时![]() >0恒成立,
>0恒成立,
![]() 在(0,1)上递减,在(1,+)上递增,所以x=1是函数
在(0,1)上递减,在(1,+)上递增,所以x=1是函数![]() 的极小值点,不满足;
的极小值点,不满足;
当![]() 即
即![]() 或
或![]() 时,
时,
![]() 在(0,1)上递减,在(1,+)上递增,所以x=1是函数
在(0,1)上递减,在(1,+)上递增,所以x=1是函数![]() 的极小值点,不满足;
的极小值点,不满足;
当![]() 时,解得
时,解得![]() 或
或![]() (舍),
(舍),
当![]() 时,设
时,设![]() 的两个零点为
的两个零点为![]() ,
,![]() ,所以
,所以![]()
![]() =1,不妨设0<
=1,不妨设0<![]() <
<![]() ,
,
又![]() ,所以0<
,所以0<![]() <1<
<1<![]() ,故
,故![]() ,
,
当x(0,![]() )时,
)时,![]() <0;当x(
<0;当x(![]() ,1)时,
,1)时,![]() >0;当x(1,
>0;当x(1,![]() )时,
)时,![]() <0;当x(
<0;当x(![]() ,)时,
,)时,![]() >0;
>0;
∴![]() 在(0,
在(0,![]() )上递减,在(
)上递减,在(![]() ,1)上递增,在(1,
,1)上递增,在(1,![]() )上递减,在(
)上递减,在(![]() ,)上递增;
,)上递增;
所以x=1是函数![]() 极大值点,满足.
极大值点,满足.
综上所述:![]() .
.
(3)①由(2)知当![]() 时,函数
时,函数![]() 在(0,1)上单调递减,在(1,)上单调递增,故函数
在(0,1)上单调递减,在(1,)上单调递增,故函数![]() 至多有两个零点,欲使
至多有两个零点,欲使![]() 有两个零点,需
有两个零点,需![]() ,得
,得![]() ,
,
![]() ;
;
![]() ,
,![]() ,
,
故满足函数有2个零点.
②当![]() 时,由(2)知
时,由(2)知![]() 在(0,
在(0,![]() )上递减,在(
)上递减,在(![]() ,1)上递增,在(1,
,1)上递增,在(1,![]() )上递减,在(
)上递减,在(![]() ,)上递增;
,)上递增;
而0<![]() <1,所以
<1,所以![]() ,
,
此时函数![]() 也至多有两个零点
也至多有两个零点
综上①②所述,函数![]() 的零点个数m的最大值为2.
的零点个数m的最大值为2.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案【题目】已知平面直角坐标系![]() ,直线
,直线![]() 过点
过点![]() ,且倾斜角为
,且倾斜角为![]() ,以
,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的参数方程和圆
的参数方程和圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的倾斜角的
的倾斜角的![]() 值.
值.
【题目】某医院对治疗支气管肺炎的两种方案![]() ,
,![]() 进行比较研究,将志愿者分为两组,分别采用方案
进行比较研究,将志愿者分为两组,分别采用方案![]() 和方案
和方案![]() 进行治疗,统计结果如下:
进行治疗,统计结果如下:
有效 | 无效 | 合计 | |
使用方案 | 96 | 120 | |
使用方案 | 72 | ||
合计 | 32 |
(1)完成上述列联表,并比较两种治疗方案有效的频率;
(2)能否在犯错误的概率不超过0.05的前提下认为治疗是否有效与方案选择有关?
附: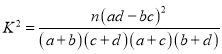 ,其中
,其中![]() .
.
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |