题目内容
【题目】关于x的实系数方程![]() 和
和![]() 有四个不同的根,若这四个根在复平面上对应的点共圆,则m的取值范围是( )
有四个不同的根,若这四个根在复平面上对应的点共圆,则m的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
根据条件分别设四个不同的解所对应的点为ABCD,讨论根的判别式,根据圆的对称性得到相应判断.
解:由已知x2﹣4x+5=0的解为![]() ,设对应的两点分别为A,B,
,设对应的两点分别为A,B,
得A(2,1),B(2,﹣1),
设x2+2mx+m=0的解所对应的两点分别为C,D,记为C(x1,y1),D(x2,y2),
(1)当△<0,即0<m<1时,![]() 的根为共轭复数,必有C、D关于x轴对称,又因为A、B关于x轴对称,且显然四点共圆;
的根为共轭复数,必有C、D关于x轴对称,又因为A、B关于x轴对称,且显然四点共圆;
(2)当△>0,即m>1或m<0时,此时C(x1,0),D(x2,0),且![]() =﹣m,
=﹣m,
故此圆的圆心为(﹣m,0),
半径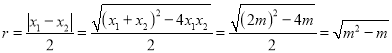 ,
,
又圆心O1到A的距离O1A=![]() ,
,
解得m=﹣1,
综上:m∈(0,1)∪{﹣1}.
故选:D.

练习册系列答案
相关题目