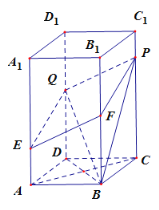
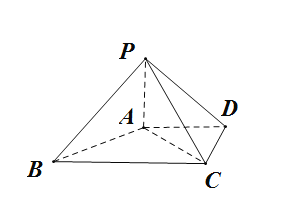
题目内容
【题目】已知数列![]() 满足奇数项
满足奇数项![]() 成等差,公差为
成等差,公差为![]() ,偶数项
,偶数项![]() 成等比,公比为
成等比,公比为![]() ,且数列
,且数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]() .
.
![]() 若
若![]() ,
,![]() .
.
①求数列![]() 的通项公式;
的通项公式;
②若![]() ,求正整数
,求正整数![]() 的值;
的值;
![]() 若
若![]() ,
,![]() ,对任意给定的
,对任意给定的![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() 对任意
对任意![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】![]() ①
①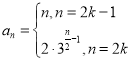 ,
,![]() ;②
;②![]() ;
;![]() 存在;
存在;![]() 的取值范围为
的取值范围为![]() .
.
【解析】
![]() 先由
先由![]() ,
,![]() ,联立求得
,联立求得![]() ,
,![]() ;①先对
;①先对![]() 进行分类(正奇数与正偶数),分别求通项公式;②先对
进行分类(正奇数与正偶数),分别求通项公式;②先对![]() 进行分类(正奇数与正偶数),利用①求得的通项公式分别求满足题意的
进行分类(正奇数与正偶数),利用①求得的通项公式分别求满足题意的![]() ,再综合;
,再综合;
![]() 分当
分当![]() 与
与![]() 两种情况分别研究,求出
两种情况分别研究,求出![]() 的取值范围.
的取值范围.
解:![]() ①因为
①因为![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,即
,即![]() 解得
解得![]() ,
,![]() .
.
当![]() 为奇数时,设
为奇数时,设![]() ,则
,则![]()
当![]() 为偶数时,设
为偶数时,设![]() ,则
,则![]()
综上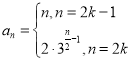 ,
,![]() .
.
②当![]() 为奇数时,
为奇数时,![]() ,即
,即![]() ,即
,即![]() ,当
,当![]() 时,不合题意;
时,不合题意;
当![]() 时,右边小于2,左边大于2,等式不成立;
时,右边小于2,左边大于2,等式不成立;
当![]() 为偶数时,
为偶数时,![]() ,
,![]() ,所以
,所以![]() .综上,
.综上,![]() .
.
![]() 当
当![]() 时,由于
时,由于![]() ,
,![]() 各项,所以
各项,所以![]() ,所以
,所以![]() 符合题意;
符合题意;
当![]() 时,假设
时,假设![]() 对任意
对任意![]() 恒成立,即
恒成立,即![]() 对任意
对任意![]() 恒成立,
恒成立,
所以![]() ,令
,令![]() ,即
,即![]() 对任意
对任意![]() 恒成立
恒成立
先证:![]() 对任意
对任意![]() 恒成立,
恒成立,
令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
所以![]() ,即
,即![]() 对任意
对任意![]() 恒成立,所以
恒成立,所以![]() ,
,
所以![]() ,所以当
,所以当![]() 时,
时,![]() ,
,
即![]() ,解得
,解得![]() ,
,
所以当![]() 且
且![]() 时,
时,![]() 这与
这与![]() 对任意
对任意![]() 恒成立矛盾,所以当
恒成立矛盾,所以当![]() 时不合题意;
时不合题意;
综上![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目