题目内容
已知函数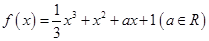 .
.
(1)求函数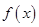 的单调区间;
的单调区间;
(2)当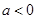 时,试讨论是否存在
时,试讨论是否存在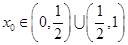 ,使得
,使得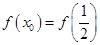 .
.
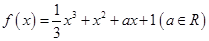 .
.(1)求函数
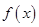 的单调区间;
的单调区间;(2)当
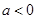 时,试讨论是否存在
时,试讨论是否存在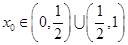 ,使得
,使得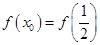 .
.(1)详见解析;(2)详见解析.
试题分析:(1)先求出导数
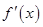 为二次函数,对
为二次函数,对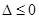 和
和 进行分类讨论,根据导数的正负求出函数
进行分类讨论,根据导数的正负求出函数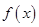 的单调区间;(2)由作差法
的单调区间;(2)由作差法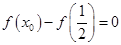 将等式进行因式分解,得到
将等式进行因式分解,得到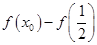
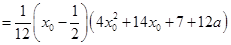 ,于是将问题转化为方程
,于是将问题转化为方程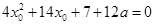 在
在 上有解,并求出该方程的两根,并判定其中一根
上有解,并求出该方程的两根,并判定其中一根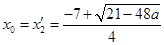 在区间
在区间 上,并由
上,并由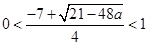 以及
以及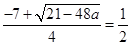 确定满足条件
确定满足条件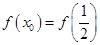 时
时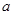 的取值范围,然后取相应的补集作为满足条件
的取值范围,然后取相应的补集作为满足条件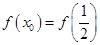 时
时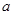 的取值范围.
的取值范围.(1)
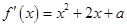 ,方程
,方程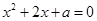 的判别式为
的判别式为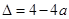 ,
,①当
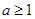 时,
时,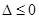 ,则
,则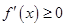 ,此时
,此时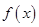 在
在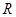 上是增函数;
上是增函数;②当
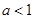 时,方程
时,方程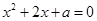 的两根分别为
的两根分别为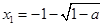 ,
,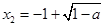 ,
,解不等式
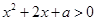 ,解得
,解得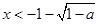 或
或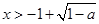 ,
,解不等式
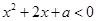 ,解得
,解得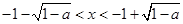 ,
,此时,函数
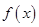 的单调递增区间为
的单调递增区间为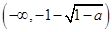 和
和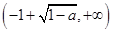 ,
,单调递减区间为
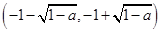 ;
;综上所述,当
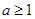 时,函数
时,函数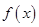 的单调递增区间为
的单调递增区间为 ,
,当
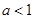 时,函数
时,函数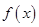 的单调递增区间为
的单调递增区间为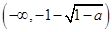 和
和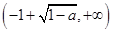 ,
,单调递减区间为
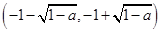 ;
;(2)
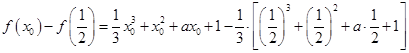
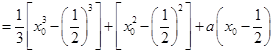
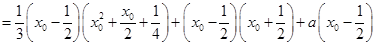
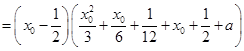
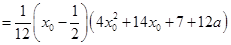 ,
,若存在
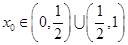 ,使得
,使得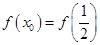 ,
,必须
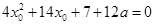 在
在 上有解,
上有解,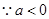 ,
,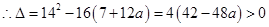 ,
,方程的两根为
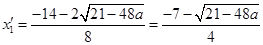 ,
,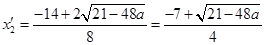 ,
,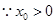 ,
,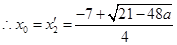 ,
,依题意,
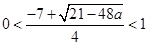 ,即
,即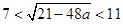 ,
,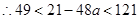 ,即
,即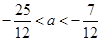 ,
,又由
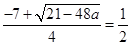 得
得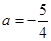 ,
,故欲使满足题意的
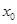 存在,则
存在,则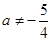 ,
,所以,当
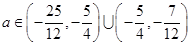 时,存在唯一
时,存在唯一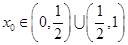 满足
满足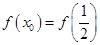 ,
,当
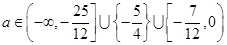 时,不存在
时,不存在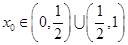 满足
满足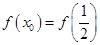 .
.
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
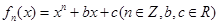 .
.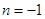 ,函数
,函数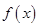 在区间
在区间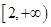 上是单调递增函数,求实数
上是单调递增函数,求实数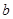 的取值范围;
的取值范围;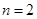 ,若对任意
,若对任意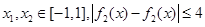 恒成立,求
恒成立,求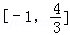
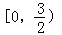
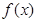 是定义在R上的奇函数,当
是定义在R上的奇函数,当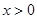 时,
时,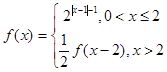 ,则
,则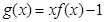 在
在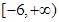 上所有零点之和为 .
上所有零点之和为 .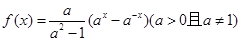
 的奇偶性;
的奇偶性;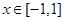 时,
时, 恒成立,求b的取值范围.
恒成立,求b的取值范围.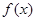 在R上存在导数
在R上存在导数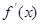 ,对任意的
,对任意的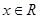 有
有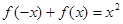 ,且在
,且在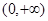 上
上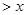 .若
.若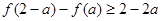 ,则实数
,则实数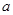 的取值范围 .
的取值范围 .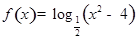 的单调递增区间是
的单调递增区间是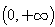
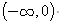
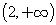
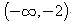
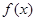 是定义在
是定义在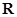 上的偶函数,且
上的偶函数,且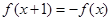 ,若
,若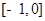 上单调递减,则
上单调递减,则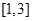 上是( )
上是( )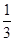 )=0,则不等式f(
)=0,则不等式f(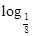 x)>0的解集是( )
x)>0的解集是( ) )
)