题目内容
1．若复数z=a-2+ai（a∈R）为纯虚数，则|a+i|=$\sqrt{5}$．分析 利用复数z=a-2+ai（a∈R）为纯虚数，得到实部为0，虚部不为0，求出a，再计算复数的模．
解答 解：因为复数z=a-2+ai（a∈R）为纯虚数，所以a-2=0并且a≠0，所以a=2，
所以|a+i|=|2+i|=$\sqrt{{2}^{2}+{1}^{2}}=\sqrt{5}$；
故答案为：$\sqrt{5}$．
点评 本题考查了复数的基本概念以及复数模的求法；关键是利用复数的基本概念求出a．
练习册系列答案
相关题目
11．
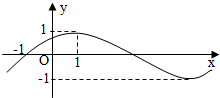已知函数f（x）=Asin（ωx+ϕ），x∈R（其中A＞0，ω＞0，-$\frac{π}{2}$＜ϕ＜$\frac{π}{2}$），其部分图象如下图所示，将f（x）的图象纵坐标不变，横坐标变成原来的$\frac{1}{2}$倍，再向右平移1个单位得到g（x）的图象，则函数g（x）的解析式为（ ）
已知函数f（x）=Asin（ωx+ϕ），x∈R（其中A＞0，ω＞0，-$\frac{π}{2}$＜ϕ＜$\frac{π}{2}$），其部分图象如下图所示，将f（x）的图象纵坐标不变，横坐标变成原来的$\frac{1}{2}$倍，再向右平移1个单位得到g（x）的图象，则函数g（x）的解析式为（ ）| A． | g（x）=sin$\frac{π}{8}$（x+1） | B． | g（x）=sin（$\frac{π}{2}$x-$\frac{π}{4}$） | C． | g（x）=sin（$\frac{π}{8}$x+1） | D． | g（x）=sin（$\frac{π}{2}$x+$\frac{π}{4}$） |
12．已知△ABC，角A，B，C所对的边分别为a，b，c，则以下为钝角三角形的是（ ）
| A． | a=3，b=3，c=4 | B． | a=4，b=5，c=6 | C． | a=4，b=6，c=7 | D． | a=3，b=3，c=5 |
16．如图是高中课程结构图：音乐所属课程是（ ）
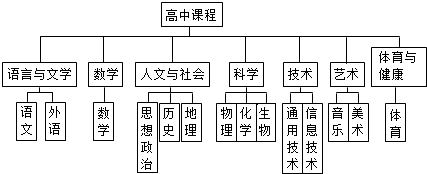
| A． | 艺术 | B． | 人文与社会 | C． | 技术 | D． | 科学 |
6．已知集合A={0，1}，则满足X⊆A的非空集合X的个数是（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
10．已知向量$\overrightarrow{a}$=（1，k），$\overrightarrow{b}$=（9，k-6），若$\overrightarrow{a}$∥$\overrightarrow{b}$，则实数k的值为（ ）
| A． | -$\frac{3}{4}$ | B． | $\frac{3}{5}$ | C． | 3 | D． | 3+3$\sqrt{2}$ |
如图，在正三棱柱（底面是正三角形的直棱柱）ABC-A1B1C1中，D为AC的中点，