题目内容
19.已知函数f(x)=x-$\frac{1}{x}$,g(x)=alnx,h(x)=f(x)-g(x).(1)若h(x)在(0,+∞)上单调递增,求a的取值范围;
(2)当a取(1)中最大值时,求函数h(x)+h(2-x)=0在(0,1)上的根的个数.
分析 (1)求导,函数h(x)在(0,+∞)上单调递增,可知x2-ax+1≥0在(0,+∞)上恒成立,即a≤x+$\frac{1}{x}$在(0,+∞)上恒成立,故只需求x+$\frac{1}{x}$的最小值.
(2)整理方程得:2-$\frac{2}{x(2-x)}$-2lnx(2-x)=0,构造函数φ(t)=2-$\frac{2}{t}$-2lnt,利用导数研究函数φ(t)的取值范围.
解答 (1)h(x)=f(x)-g(x)=x-$\frac{1}{x}$-alnx(x>0),
∴h'(x)=$\frac{{x}^{2}-ax+1}{{x}^{2}}$
∵函数h(x)在(0,+∞)上单调递增,
∴x2-ax+1≥0在(0,+∞)上恒成立,即a≤x+$\frac{1}{x}$在(0,+∞)上恒成立,
解得a≤2;
(2)当a=2时,h(x)=x-$\frac{1}{x}$-2lnx,
∴h(x)+h(2-x)=2-$\frac{2}{x(2-x)}$-2lnx(2-x).
令t=x(2-x),t∈(0,1),
构造函数φ(t)=2-$\frac{2}{t}$-2lnt,
∴φ'(t)=$\frac{2-2t}{{t}^{2}}$>0恒成立,
∴函数φ(t)在(0,1)上单调递增,且φ(1)=0,
∴φ(t)=2-$\frac{2}{t}$-2lnt在(0,1)上无解.
故函数h(x)+h(2-x)=0在(0,1)上的根的个数为零.
点评 考察了利用导数研究函数的单调性;构造函数,利用导数研究函数的极值.

练习册系列答案
相关题目
8.下列各图中表示的由A到B的对应能构成映射的个数是( )
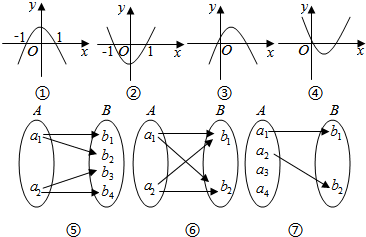

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |