Question

4．已知正方体ABCD-A₁B₁C₁D₁，E为BC的中点，求B₁E与平面AD₁C所成角．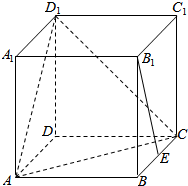

Answer 1

分析 以D为原点，DA为x轴，DC为y轴，DD₁为z轴，建立空间直角坐标系，利用向量法能求出B₁E与平面AD₁C所成角．

解答 解：以D为原点，DA为x轴，DC为y轴，DD₁为z轴，建立空间直角坐标系，
设正方体ABCD-A₁B₁C₁D₁的棱长为2，
由A（2，0，0），C（0，2，0），E（1，2，0），D₁（0，0，2），B₁（2，2，2），
$\overrightarrow{A{D}_{1}}$=（-2，0，2），$\overrightarrow{AC}$=（-2，2，0），B₁E=（-1，0，-2），
设平面ACD₁的法向量$\overrightarrow{n}$=（x，y，z），
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{A{D}_{1}}=-2x+2z=0}\\{\overrightarrow{n}•\overrightarrow{AC}=-2x+2y=0}\end{array}\right.$，取x=1，得$\overrightarrow{n}$=（1，1，1），
设B₁E与平面AD₁C所成角为θ，
则sinθ=|cos＜$\overrightarrow{{B}_{1}E}，\overrightarrow{n}$＞|=|$\frac{-1+0-2}{\sqrt{5}•\sqrt{3}}$|=$\frac{\sqrt{15}}{5}$，
∴B₁E与平面AD₁C所成角为arcsin$\frac{\sqrt{15}}{5}$．

点评 本题考查线面角的求法，是中档题，解题时要认真审题，注意向量法的合理运用．