题目内容
20.求函数y=|x-1|+|x+1|(x∈(-2,3])的值域.分析 化简函数的解析式,结合x的范围,利用函数的单调性求得函数的值域.
解答 解:∵函数y=|x-1|+|x+1|=$\left\{\begin{array}{l}{-2x,-2<x<-1}\\{2,-1≤x≤1}\\{2x,1<x≤3}\end{array}\right.$,
且f(-2)=4,f(3)=6,且函数在(-2,-1)上单调递减、在[-1,1]上为常数2,
在(1,3]上单调递增,
故函数y=|x-1|+|x+1|(x∈(-2,3])的值域为[2,6].
点评 本题主要考查带有绝对值的函数,分段函数的应用,利用函数的单调性求函数的值域,属于中档题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
8.下列各图中表示的由A到B的对应能构成映射的个数是( )
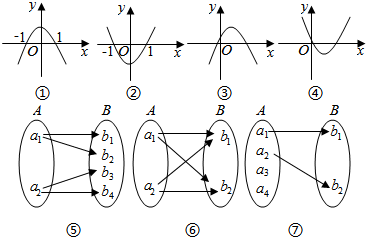

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
5.已知公差不为0的等差数列{an}满足a1,a3,a4成等比数列,Sn为{an}的前n项和,则$\frac{{{S_3}-{S_2}}}{{{S_5}-{S_3}}}$的值为( )
| A. | 2 | B. | 3 | C. | $\frac{1}{5}$ | D. | 4 |