题目内容
已知正项数列{an}的前n项和为Sn,且a1=1,an=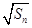 +
+ (n≥2),则数列{an}的通项公式为an=( )
(n≥2),则数列{an}的通项公式为an=( )
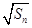 +
+ (n≥2),则数列{an}的通项公式为an=( )
(n≥2),则数列{an}的通项公式为an=( )| A.n-1 | B.n | C.2n-1 | D.2n |
C
由已知可得Sn-Sn-1=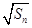 +
+ (n≥2),又
(n≥2),又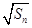 +
+ >0,故
>0,故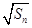 -
- =1,所以数列{
=1,所以数列{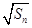 }是等差数列,其公差为1,首项
}是等差数列,其公差为1,首项 =1,故
=1,故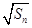 =n,即Sn=n2,当n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1,当n=1时也适合上式,故数列{an}的通项公式为an=2n-1,选C.
=n,即Sn=n2,当n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1,当n=1时也适合上式,故数列{an}的通项公式为an=2n-1,选C.
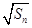 +
+ (n≥2),又
(n≥2),又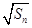 +
+ >0,故
>0,故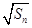 -
- =1,所以数列{
=1,所以数列{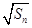 }是等差数列,其公差为1,首项
}是等差数列,其公差为1,首项 =1,故
=1,故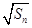 =n,即Sn=n2,当n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1,当n=1时也适合上式,故数列{an}的通项公式为an=2n-1,选C.
=n,即Sn=n2,当n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1,当n=1时也适合上式,故数列{an}的通项公式为an=2n-1,选C.
练习册系列答案
相关题目
 的前n项和为
的前n项和为 ,且
,且
 ,令
,令 .
. 是等差数列,并求数列
是等差数列,并求数列
 是18的倍数.
是18的倍数.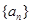 的公差为d,若数列
的公差为d,若数列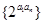 为递减数列,则( )
为递减数列,则( )



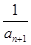 +
+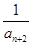 +
+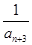 +…+
+…+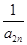 ,若对任意的正整数n,当m∈[-1,1]时,不等式t2-2mt+
,若对任意的正整数n,当m∈[-1,1]时,不等式t2-2mt+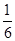 >bn恒成立,求实数t的取值范围.
>bn恒成立,求实数t的取值范围. }中,
}中, ,前
,前 项和
项和 .
. 项、第
项、第 项、第
项、第 项…第
项…第 项……按原来的顺序组成一个新的数列{
项……按原来的顺序组成一个新的数列{ },求数列{
},求数列{ 项和
项和 .
. 的前
的前 项和为
项和为 ,
, ,
,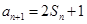 ,等差数列
,等差数列 满足
满足 ,
, .
. ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.