Question

【题目】已知关于x的一元二次方程x2﹣2ax+a+2=0，当a为何值时，该方程：
（1）有两个不同的正根；
（2）有不同的两根且两根在（1，3）内．

Answer 1

【答案】
（1）解：关于x的一元二次方程x2﹣2ax+a+2=0，

当△=4a2﹣4（a+2）＞0，且x1+x2=2a＞0、x1x2=a+2＞0时，

即当a＞2时，该方程有两个不同的正根

（2）解：令f（x）=x2﹣2ax+a+2，则当 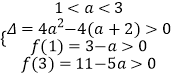时，即2＜a＜ 时，

方程x2﹣2ax+a+2=0有不同的两根且两根在（1，3）内

【解析】（1）方程有两个不同的正根，等价于△=4a2﹣4（a+2）＞0，且x1+x2=2a＞0、x1x2=a+2＞0．由此求得a的范围．（2）令f（x）=x2﹣2ax+a+2，则当 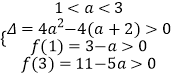时，满足条件，由此求得a的范围．