��Ŀ����
8������������ԭ�㣬����һ������Ϊ��$\sqrt{3}$��0����������Ϊ$\frac{\sqrt{3}}{2}$��Բ�����ҽ���ΪF1��F2����������Բ�ı����̣�
������P�Ǹ���Բ�ϵ�һ�����㣬��$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$�����ֵ����Сֵ��
�����������M��0��2����ֱ��l����Բ���ڲ�ͬ������A��B���ҡ�AOBΪ��ǣ�����OΪ����ԭ�㣩����ֱ��l��б��k��ȡֵ��Χ��
���� ��������Բ�Ķ��������Բ���̣�
���������⣬���a��b��c��ֵ��Ȼ����P�����꣬����PF1•PF2�ı���ʽ������һԪ���κ�������ֵ������⣮
�������ֱ�߷��̣�����֪��Բ���������飬�����������Τ�ﶨ��������Ĺ�ϵ�����k��ȡֵ��Χ��
��� �⣺��������һ������Ϊ��$\sqrt{3}$��0����������Ϊ$\frac{\sqrt{3}}{2}$����c=$\sqrt{3}$��$\frac{c}{a}=\frac{\sqrt{3}}{2}$��
��a=2��b=1
����Բ����Ϊ$\frac{{x}^{2}}{4}+{y}^{2}=1$
������������֪������Ϊ��$\sqrt{3}$��0������-$\sqrt{3}$��0������P��x��y����
��$\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}=��-\sqrt{3}-x��-y��•��\sqrt{3}-x��-y��$=${x}^{2}+{y}^{2}-3={x}^{2}+1-\frac{{x}^{2}}{4}-3=\frac{1}{4}��3{x}^{2}-8��$
��Ϊx��[-2��2]��
�ʵ�x=0������PΪ��Բ����˵�ʱ��
$\overrightarrow{P{F}_{1}}$����Сֵ-2
��x=��2������PΪ��Բ����˵�ʱ��
$\overrightarrow{P{F}_{1}}$�����ֵ1
������Ȼֱ��x=0����������������
����ֱ��l��y=kx+2��A��x1��y1����B��x2��y2����
����$\left\{\begin{array}{l}{y=kx+2}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$����ȥy�������ã�$��{k}^{2}+\frac{1}{4}��{x}^{2}+4kx+3=0$
��${x}_{1}+{x}_{2}=-\frac{4k}{{k}^{2}+\frac{1}{4}}��{x}_{1}{x}_{2}=\frac{3}{{k}^{2}+\frac{1}{4}}$
�ɡ�=$��4k��^{2}-4��{k}^{2}+\frac{1}{4}����3=4{k}^{2}-3��0$�ã�$k��-\frac{\sqrt{3}}{2}$��$k��\frac{\sqrt{3}}{2}$��
��0�㣼��AOB��90��?��cos��AOB��0cos��AOB��0?$\overrightarrow{OA}•\overrightarrow{OB}��0$
��$\overrightarrow{OA}•\overrightarrow{OB}={x}_{1}{x}_{2}+{y}_{1}{y}_{2}��0$
��y1y2=��kx1+2����kx2+2��
=k2x1x2+2k��x1+x2��+4
=$\frac{3{k}^{2}}{{k}^{2}+\frac{1}{4}}+\frac{-8{k}^{2}}{{k}^{2}+\frac{1}{4}}+4=\frac{-{k}^{2}+1}{{k}^{2}+\frac{1}{4}}$
��$\frac{3}{{k}^{2}+\frac{1}{4}}+\frac{-{k}^{2}+1}{{k}^{2}+\frac{1}{4}}��0$
��k2��4����-2��k��2��
���ɢ١��ڵã�
$-2��k��-\frac{\sqrt{3}}{2}$��$\frac{\sqrt{3}}{2}��k��2$
���� ������Ҫ����ֱ�ߡ���Բ��ƽ���������������Ȼ���֪ʶ���Լ��ۺ�Ӧ����ѧ֪ʶ������⼰������������������Ϊ�е��⣬��Ҫ���������������Τ�ﶨ����

| A�� | x2-$\frac{y^2}{9}$=1 | B�� | x2-y2=15 | C�� | $\frac{x^2}{9}-{y^2}$=1 | D�� | x2-y2=9 |
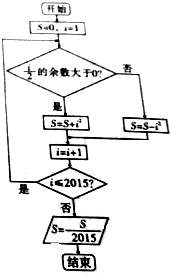
| A�� | 1006 | B�� | 1008 | C�� | 2015 | D�� | 2016 |
| A�� | $\frac{{\sqrt{5}}}{4}$ | B�� | $\frac{{\sqrt{6}}}{6}$ | C�� | $\frac{{\sqrt{5}}}{6}$ | D�� | 2 |