题目内容
【题目】已知椭圆
＋
＝1(a>b>0)的焦点分别为F1(0，－1)，F2(0,1)，且3a2＝4b2.
(1)求椭圆的方程；
(2)设点P在这个椭圆上，且|PF1|－|PF2|＝1，求∠F1PF2的余弦值．
【答案】（1）
＋
＝1.（2）
【解析】分析：（1）利用已知条件求出
，然后求解
，
，即可得到椭圆方程；（2）利用椭圆的定义以及已知条件，求出三角形的边长，利用余弦定理转化求解即可．
详解：(1)由题意得椭圆焦点在y轴上，且c＝1.
又∵3a2＝4b2，
∴a2－b2＝
a2＝c2＝1，
∴a2＝4，b2＝3，
∴椭圆的标准方程为＋＝1.
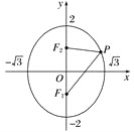
(2)如图所示，|PF1|－|PF2|＝1.
又由椭圆定义知，|PF1|＋|PF2|＝4，
∴|PF1|＝
，|PF2|＝
，|F1F2|＝2，
∴cos∠F1PF2＝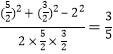
.
练习册系列答案
相关题目
