题目内容
【题目】已知函数 ![]() .
.
(1)用五点作图法画出![]() 在长度为一个周期的区间上的图象;
在长度为一个周期的区间上的图象;

(2))求函数![]() 的单调递增区间;
的单调递增区间;
(3)简述如何由![]() 的图象经过适当的图象变换得到
的图象经过适当的图象变换得到![]() 的图象?
的图象?
【答案】(1)见解析; (2) ![]() ;(3)向左平移个
;(3)向左平移个![]() 单位,把横坐标伸长为原来的3倍,把纵坐标扩大为原来的2倍。
单位,把横坐标伸长为原来的3倍,把纵坐标扩大为原来的2倍。
【解析】
(1)根据三角变换将函数解析式化为![]() 后再根据“五点法”画出函数的图象;(2)将
后再根据“五点法”画出函数的图象;(2)将![]() 作为整体,并根据正弦函数的单调增区间可得所求;(3)根据变换前后两函数解析式的特点可写出变换的过程.
作为整体,并根据正弦函数的单调增区间可得所求;(3)根据变换前后两函数解析式的特点可写出变换的过程.
(1)![]()
![]()
![]()
![]() .
.
列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
画出图象如图所示:
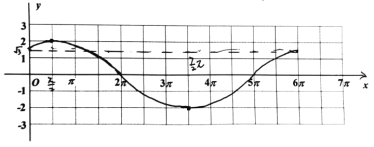
(2)由![]() ,
,
得![]() ,
,
所以函数![]() 的单调增区间为
的单调增区间为![]() .
.
(3)把函数![]() 的图象向左平移
的图象向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象;再把所得图象上所有点的横坐标伸长为原来的3倍(纵坐标不变),得到函数
的图象;再把所得图象上所有点的横坐标伸长为原来的3倍(纵坐标不变),得到函数![]() 的图象;再把所得图象上所有点的纵坐标扩大为原来的2倍(横坐标不变),得到函数
的图象;再把所得图象上所有点的纵坐标扩大为原来的2倍(横坐标不变),得到函数![]() 的图象.
的图象.

练习册系列答案
相关题目
【题目】在十九大“建设美丽中国”的号召下,某省级生态农业示范县大力实施绿色生产方案,对某种农产品的生产方式分别进行了甲、乙两种方案的改良。为了检查甲、乙两种方案的改良效果,随机在这两种方案中各任意抽取了![]() 件产品作为样本逐件称出它们的重量(单位:克),重量值落在
件产品作为样本逐件称出它们的重量(单位:克),重量值落在![]() 之间的产品为合格品,否则为不合格品。下表是甲、乙两种方案样本频数分布表。
之间的产品为合格品,否则为不合格品。下表是甲、乙两种方案样本频数分布表。
产品重量 | 甲方案频数 | 乙方案频数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)求出甲(同组中的重量值用组中点值代替)方案样本中![]() 件产品的平均数;
件产品的平均数;
(2)若以频率作为概率,试估计从两种方案分别任取![]() 件产品,恰好两件产品都是合格品的概率分别是多少;
件产品,恰好两件产品都是合格品的概率分别是多少;
(3)由以上统计数据完成下面![]() 列联表,并回答有多大把握认为“产品是否为合格品与改良方案的选择有关”.
列联表,并回答有多大把握认为“产品是否为合格品与改良方案的选择有关”.
甲方案 | 乙方案 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
参考公式: 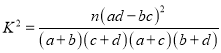 ,其中
,其中![]() .
.
临界值表:
|
|
|
|
|
|
|
|
|
|
|
|