题目内容
【题目】已知曲线![]() 是中心在原点,焦点在
是中心在原点,焦点在![]() 轴上的双曲线的右支,它的离心率刚好是其对应双曲线的实轴长,且一条渐近线方程是
轴上的双曲线的右支,它的离心率刚好是其对应双曲线的实轴长,且一条渐近线方程是![]() ,线段
,线段![]() 是过曲线
是过曲线![]() 右焦点
右焦点![]() 的一条弦,
的一条弦,![]() 是弦
是弦![]() 的中点。
的中点。
(1)求曲线![]() 的方程;
的方程;
(2)求点![]() 到
到![]() 轴距离的最小值;
轴距离的最小值;
(3)若作出直线![]() ,
,![]() 使点
使点![]() 在直线
在直线![]() 上的射影
上的射影![]() 满足
满足![]() .当点
.当点![]() 在曲线
在曲线![]() 上运动时,求
上运动时,求![]() 的取值范围.
的取值范围.
(参考公式:若![]() 为双曲线
为双曲线![]() 右支上的点,
右支上的点,![]() 为右焦点,则
为右焦点,则![]() .(
.(![]() 为离心率))
为离心率))
【答案】(1)![]() ; (2)点
; (2)点![]() 到
到![]() 轴距离的最小值为
轴距离的最小值为![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据已知设双曲线的右支方程,离心率刚好是其对应双曲线的实轴长,可以得到![]() 的关系,一条渐近线方程是
的关系,一条渐近线方程是![]() ,可以得到
,可以得到![]() 的关系,而
的关系,而![]() ,三个等式联立,可以求出
,三个等式联立,可以求出![]() 的值,最后求出双曲线的右支方程,别忘记写上
的值,最后求出双曲线的右支方程,别忘记写上![]() 的取值范围。
的取值范围。
(2)根据斜率是否存在进行分类讨论:当存在斜率时,设出直线方程与双曲线右支方程联立,求出满足条件的斜率取值范围,根据一元二次方程根与系数的关系求出点![]() 的横坐标的大小,求出点
的横坐标的大小,求出点![]() 到
到![]() 轴距离的取值范围。当不存在斜率时,求出点
轴距离的取值范围。当不存在斜率时,求出点![]() 到
到![]() 轴距离,综合两种情形得出结论。
轴距离,综合两种情形得出结论。
(3)由![]() 可以得到
可以得到![]() ,这样可以求出
,这样可以求出![]() 与
与![]() 的关系,由焦半径公式可以求出
的关系,由焦半径公式可以求出![]() ,两个式子联立,可以求出
,两个式子联立,可以求出![]() 点的横坐标,利用(2)的结论,可以求出
点的横坐标,利用(2)的结论,可以求出![]() 的取值范围。
的取值范围。
(1)设![]() ,离心率刚好是其对应双曲线的实轴长,所以有
,离心率刚好是其对应双曲线的实轴长,所以有![]() ①,一条渐近线方程是
①,一条渐近线方程是![]() 所以有
所以有![]() ②,而
②,而![]() ③,三个方程联立,可求出
③,三个方程联立,可求出![]() ,所以曲线
,所以曲线![]() 的方程是:
的方程是:![]()
(2)由(1)知,曲线![]() 的右焦点
的右焦点![]() 的坐标为
的坐标为![]() ,若弦
,若弦![]() 的斜率存在,
的斜率存在,
则弦![]() 的方程为:
的方程为:![]() ,代入双曲线方程得:
,代入双曲线方程得:
![]() .
.
设点![]() ,
, ![]() ,
,
由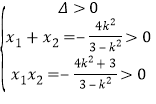 ,解得:
,解得:![]() ,点
,点![]() 到
到![]() 轴距离:
轴距离:
![]()
而当弦![]() 的斜率不存在时,点
的斜率不存在时,点![]() 到
到![]() 轴距离
轴距离![]() 。
。
所以点![]() 到
到![]() 轴距离的最小值为
轴距离的最小值为![]() .
.
(3)![]() 点
点![]() 在直线
在直线![]() 上的射影
上的射影![]() 满足
满足![]() ,
,
![]() ,
,![]() 到直线
到直线![]() 的距离
的距离![]() ……①
……①
由焦半径公式![]()
![]()
![]() ……②
……②
将②代入①,得:![]()
![]() ,
,![]() ,
, ![]() .
.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目







