题目内容
【题目】已知函数![]() ,
, ![]()
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调递减区间;
的单调递减区间;
(Ⅱ)若![]() 时,关于
时,关于![]() 的不等式
的不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若数列![]() 满足
满足![]() ,
, ![]() ,记
,记![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证: ![]() .
.
【答案】(I)![]() ;(II)
;(II)![]() ;(III)证明见解析.
;(III)证明见解析.
【解析】试题分析:(Ⅰ)求出![]() ,在定义域内,分别令
,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间, ![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(Ⅱ)当
的减区间;(Ⅱ)当![]() 时,因为
时,因为![]() ,所以
,所以![]() 显然不成立,先证明因此
显然不成立,先证明因此![]() 时,
时, ![]() 在
在![]() 上恒成立,再证明当
上恒成立,再证明当![]() 时不满足题意,从而可得结果;(III)先求出等差数列的前
时不满足题意,从而可得结果;(III)先求出等差数列的前![]() 项和为
项和为![]() ,结合(II)可得
,结合(II)可得![]() ,各式相加即可得结论.
,各式相加即可得结论.
试题解析:(Ⅰ)由![]() ,得
,得![]() .所以
.所以![]()
令![]() ,解得
,解得![]() 或
或![]() (舍去),所以函数
(舍去),所以函数![]() 的单调递减区间为
的单调递减区间为 ![]() .
.
(Ⅱ)由![]() 得,
得, ![]()
当![]() 时,因为
时,因为![]() ,所以
,所以![]() 显然不成立,因此
显然不成立,因此![]() .
.
令![]() ,则
,则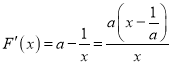 ,令
,令![]() ,得
,得![]() .
.
当![]() 时,
时, ![]() ,
, ![]() ,∴
,∴![]() ,所以
,所以![]() ,即有
,即有![]() .
.
因此![]() 时,
时, ![]() 在
在![]() 上恒成立.
上恒成立.
②当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,
∴![]() ,不满足题意.
,不满足题意.
综上,不等式![]() 在
在![]() 上恒成立时,实数
上恒成立时,实数![]() 的取值范围是
的取值范围是![]() .
.
(III)证明:由![]() 知数列
知数列![]() 是
是![]() 的等差数列,所以
的等差数列,所以![]()
所以![]()
由(Ⅱ)得, ![]() 在
在![]() 上恒成立.
上恒成立.
所以![]() . 将以上各式左右两边分别相加,得
. 将以上各式左右两边分别相加,得
![]() .因为
.因为![]()
所以![]()
所以![]() .
.
【题型】解答题
【/span>结束】
22
【题目】已知直线![]() , (
, (![]() 为参数,
为参数, ![]() 为倾斜角).以坐标原点为极点,
为倾斜角).以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(Ⅰ)将曲线![]() 的直角坐标方程化为极坐标方程;
的直角坐标方程化为极坐标方程;
(Ⅱ)设点![]() 的直角坐标为
的直角坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() 、
、![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(I)![]() ;(II)
;(II)![]() .
.
【解析】试题分析:(Ⅰ)将由![]() 代入
代入![]() ,化简即可得到曲线
,化简即可得到曲线![]() 的极坐标方程;(Ⅱ)将
的极坐标方程;(Ⅱ)将![]() 的参数方程
的参数方程![]() 代入
代入![]() ,得
,得![]() ,根据直线参数方程的几何意义,利用韦达定理结合辅助角公式,由三角函数的有界性可得结果.
,根据直线参数方程的几何意义,利用韦达定理结合辅助角公式,由三角函数的有界性可得结果.
试题解析:(Ⅰ)由![]() 及
及![]() ,得
,得![]() ,即
,即![]()
所以曲线![]() 的极坐标方程为
的极坐标方程为![]()
(II)将![]() 的参数方程
的参数方程![]() 代入
代入![]() ,得
,得![]()
∴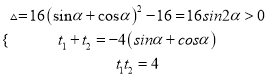 , 所以
, 所以![]() ,又
,又![]() ,
,
所以![]() ,且
,且![]() ,
,
所以![]() ,
,
由![]() ,得
,得![]() ,所以
,所以![]() .
.
故![]() 的取值范围是
的取值范围是![]() .
.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案【题目】近年来郑州空气污染较为严重,现随机抽取一年(365天)内100天的空气中![]() 指数的监测数据,统计结果如下:
指数的监测数据,统计结果如下:
|
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
记某企业每天由空气污染造成的经济损失为![]() (单位:元),
(单位:元),![]() 指数为
指数为![]() .当
.当![]() 在区间
在区间![]() 内时对企业没有造成经济损失;当
内时对企业没有造成经济损失;当![]() 在区间
在区间![]() 内时对企业造成经济损失成直线模型(当
内时对企业造成经济损失成直线模型(当![]() 指数为150时造成的经济损失为500元,当
指数为150时造成的经济损失为500元,当![]() 指数为200时,造成的经济损失为700元);当
指数为200时,造成的经济损失为700元);当![]() 指数大于300时造成的经济损失为2000元.
指数大于300时造成的经济损失为2000元.
(1)试写出![]() 的表达式;
的表达式;
(2)试估计在本年内随机抽取一天,该天经济损失![]() 大于500元且不超过900元的概率;
大于500元且不超过900元的概率;
(3)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面列联表,并判断是否有![]() 的把握认为郑州市本年度空气重度污染与供暖有关?
的把握认为郑州市本年度空气重度污染与供暖有关?
附:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.32 | 2.07 | 2.70 | 3.74 | 5.02 | 6.63 | 7.87 | 10.828 |
![]() ,其中
,其中![]() .
.
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |
【题目】甲、乙两家销售公司拟各招聘一名产品推销员,日工资方案如下: 甲公司规定底薪80元,每销售一件产品提成1元; 乙公司规定底薪120元,日销售量不超过45件没有提成,超过45件的部分每件提成8元.
(I)请将两家公司各一名推销员的日工资![]() (单位: 元) 分别表示为日销售件数
(单位: 元) 分别表示为日销售件数![]() 的函数关系式;
的函数关系式;
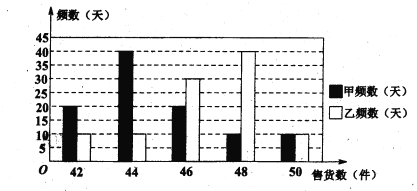
(II)从两家公司各随机选取一名推销员,对他们过去100天的销售情况进行统计,得到如下条形图。若记甲公司该推销员的日工资为![]() ,乙公司该推销员的日工资为
,乙公司该推销员的日工资为![]() (单位: 元),将该频率视为概率,请回答下面问题:
(单位: 元),将该频率视为概率,请回答下面问题:
某大学毕业生拟到两家公司中的一家应聘推销员工作,如果仅从日均收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.
【答案】(I)见解析; (Ⅱ)见解析.
【解析】分析:(I)依题意可得甲公司一名推销员的工资与销售件数的关系是一次函数的关系式,而乙公司是分段函数的关系式,由此解得;(Ⅱ)分别根据条形图求得甲、乙公司一名推销员的日工资的分布列,从而可分别求得数学期望,进而可得结论.
详解:(I)由题意得,甲公司一名推销员的日工资![]() (单位:元) 与销售件数
(单位:元) 与销售件数![]() 的关系式为:
的关系式为: ![]() .
.
乙公司一名推销员的日工资![]() (单位: 元) 与销售件数
(单位: 元) 与销售件数![]() 的关系式为:
的关系式为: 
(Ⅱ)记甲公司一名推销员的日工资为![]() (单位: 元),由条形图可得
(单位: 元),由条形图可得![]() 的分布列为
的分布列为
| 122 | 124 | 126 | 128 | 130 |
| 0.2 | 0.4 | 0.2 | 0.1 | 0.1 |
记乙公司一名推销员的日工资为![]() (单位: 元),由条形图可得
(单位: 元),由条形图可得![]() 的分布列为
的分布列为
| 120 | 128 | 144 | 160 |
| 0.2 | 0.3 | 0.4 | 0.1 |
∴![]()
∴仅从日均收入的角度考虑,我会选择去乙公司.
点睛:求解离散型随机变量的数学期望的一般步骤为:
第一步是“判断取值”,即判断随机变量的所有可能取值,以及取每个值所表示的意义;
第二步是“探求概率”,即利用排列组合,枚举法,概率公式,求出随机变量取每个值时的概率;
第三步是“写分布列”,即按规范形式写出分布列,并注意用分布列的性质检验所求的分布列或某事件的概率是否正确;
第四步是“求期望值”,一般利用离散型随机变量的数学期望的定义求期望的值
【题型】解答题
【结束】
19
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点.
的中点.
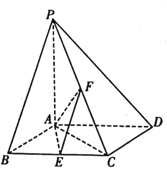
(1)证明: ![]() ;
;
(2)设![]() 为线段
为线段![]() 上的动点,若线段
上的动点,若线段![]() 长的最小值为
长的最小值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【题目】近年电子商务蓬勃发展, ![]() 年某网购平台“双
年某网购平台“双![]() ”一天的销售业绩高达
”一天的销售业绩高达![]() 亿元人民币,平台对每次成功交易都有针对商品和快递是否满意的评价系统.从该评价系统中选出
亿元人民币,平台对每次成功交易都有针对商品和快递是否满意的评价系统.从该评价系统中选出![]() 次成功交易,并对其评价进行统计,网购者对商品的满意率为
次成功交易,并对其评价进行统计,网购者对商品的满意率为![]() ,对快递的满意率为
,对快递的满意率为![]() ,其中对商品和快递都满意的交易为
,其中对商品和快递都满意的交易为![]() 次.
次.
(1)根据已知条件完成下面的![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“网购者对商品满意与对快递满意之间有关系”?
的把握认为“网购者对商品满意与对快递满意之间有关系”?
对快递满意 | 对快递不满意 | 合计 | |
对商品满意 |
| ||
对商品不满意 | |||
合计 |
|
(2)为进一步提高购物者的满意度,平台按分层抽样方法从中抽取![]() 次交易进行问卷调查,详细了解满意与否的具体原因,并在这
次交易进行问卷调查,详细了解满意与否的具体原因,并在这![]() 次交易中再随机抽取
次交易中再随机抽取![]() 次进行电话回访,听取购物者意见.求电话回访的
次进行电话回访,听取购物者意见.求电话回访的![]() 次交易至少有一次对商品和快递都满意的概率.
次交易至少有一次对商品和快递都满意的概率.
附: 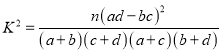 (其中
(其中![]() 为样本容量)
为样本容量)
|
|
|
|
|
|
|
|
|
|
|
|


