题目内容
【题目】如图,已知三棱锥O-ABC的三条侧棱OA,OB,OC两两垂直, ![]() 为等边三角形,
为等边三角形, ![]() 为
为![]() 内部一点,点
内部一点,点![]() 在
在![]() 的延长线上,且PA=PB.
的延长线上,且PA=PB.
(Ⅰ)证明:OA=OB;
(Ⅱ)证明:平面PAB平面POC.

【答案】(1)见解析(2)见解析
【解析】试题分析:(1)由OA,OB,OC两两垂直得![]() ,由
,由![]() 为等边三角形得OA=OB,(2)取
为等边三角形得OA=OB,(2)取![]() 的中点
的中点![]() ,则由等腰三角形性质得
,则由等腰三角形性质得![]() ,再由线面垂直判定定理得
,再由线面垂直判定定理得![]() 平面
平面![]() ,所以
,所以![]() ,再根据OA,OB,OC两两垂直得
,再根据OA,OB,OC两两垂直得![]()
![]() ,因此
,因此![]() 平面
平面![]() ,最后根据面面垂直判定定理得结论.
,最后根据面面垂直判定定理得结论.
试题解析:
证明:(Ⅰ)因为![]() ,
,![]() ,
,![]() 两两垂直,
两两垂直,
所以![]() ,
,![]()
又△![]() 为等边三角形,
为等边三角形,![]()
所以![]()
![]()
故![]()
(Ⅱ)因为![]() ,
,![]() ,
,![]() 两两垂直
两两垂直
所以![]() 平面
平面![]()
![]() 平面
平面![]() ,所以
,所以![]()
![]()
 取
取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]()
因为![]() ,
,![]() ,所以
,所以![]()
![]() ,所以
,所以![]() 平面
平面![]()
所以![]()
又![]() ,所以
,所以![]() 平面
平面![]()
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]()

练习册系列答案
相关题目
【题目】近年电子商务蓬勃发展, ![]() 年某网购平台“双
年某网购平台“双![]() ”一天的销售业绩高达
”一天的销售业绩高达![]() 亿元人民币,平台对每次成功交易都有针对商品和快递是否满意的评价系统.从该评价系统中选出
亿元人民币,平台对每次成功交易都有针对商品和快递是否满意的评价系统.从该评价系统中选出![]() 次成功交易,并对其评价进行统计,网购者对商品的满意率为
次成功交易,并对其评价进行统计,网购者对商品的满意率为![]() ,对快递的满意率为
,对快递的满意率为![]() ,其中对商品和快递都满意的交易为
,其中对商品和快递都满意的交易为![]() 次.
次.
(1)根据已知条件完成下面的![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“网购者对商品满意与对快递满意之间有关系”?
的把握认为“网购者对商品满意与对快递满意之间有关系”?
对快递满意 | 对快递不满意 | 合计 | |
对商品满意 |
| ||
对商品不满意 | |||
合计 |
|
(2)为进一步提高购物者的满意度,平台按分层抽样方法从中抽取![]() 次交易进行问卷调查,详细了解满意与否的具体原因,并在这
次交易进行问卷调查,详细了解满意与否的具体原因,并在这![]() 次交易中再随机抽取
次交易中再随机抽取![]() 次进行电话回访,听取购物者意见.求电话回访的
次进行电话回访,听取购物者意见.求电话回访的![]() 次交易至少有一次对商品和快递都满意的概率.
次交易至少有一次对商品和快递都满意的概率.
附: 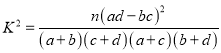 (其中
(其中![]() 为样本容量)
为样本容量)
|
|
|
|
|
|
|
|
|
|
|
|


