题目内容
6.在极坐标系中,直线l经过圆ρ=4cosθ的圆心且与直线ρcosθ=4平行,则直线l与极轴的交点的极坐标为(2,0).分析 利用$\left\{\begin{array}{l}{{ρ}^{2}={x}^{2}+{y}^{2}}\\{x=ρcosθ}\end{array}\right.$把ρ=4cosθ化为直角坐标方程可得圆心为(2,0),直线ρcosθ=4化为直角坐标方程x=4,可得直线l方程为x=2,即可得出直线l与极轴的交点的极坐标.
解答 解:ρ=4cosθ化为直角坐标方程(x-2)2+y2=4,圆心为(2,0),直线ρcosθ=4化为直角坐标方程x=4,
∴直线l方程为x=2,直线l与极轴的交点的极坐标为(2,0).
故答案为:(2,0).
点评 本题考查了极坐标方程化为直角坐标方程、相互平行的直线之间的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.阅读如图所示的程序框图,若输入m=6,则输出S等于( )
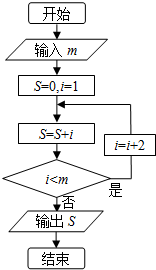

| A. | 4 | B. | 9 | C. | 16 | D. | 25 |
11.设集合S=$\left\{{x|\frac{1}{2}<{2^x}<8}\right\}$,T={x|x<a或x>a+2},S∪T=R,则a的取值范围为( )
| A. | (-1,1) | B. | [-1,1] | C. | (-∞,-1)∪(1,+∞) | D. | (-∞,-1]∪[1,+∞) |