题目内容
3.△ABC满足AB=AC,BC=2,G为△ABC的重心,则$\overrightarrow{BG}•\overrightarrow{BC}$=2.分析 如图所示,$\overrightarrow{BG}=\overrightarrow{BD}+\overrightarrow{DG}$,$\overrightarrow{BD}=\frac{1}{2}\overrightarrow{BC}$,$\overrightarrow{DG}•\overrightarrow{BC}$=0,代入展开即可得出.
解答 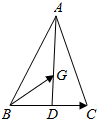 解:如图所示,
解:如图所示,
∵$\overrightarrow{BG}=\overrightarrow{BD}+\overrightarrow{DG}$,$\overrightarrow{BD}=\frac{1}{2}\overrightarrow{BC}$,$\overrightarrow{DG}•\overrightarrow{BC}$=0,
∴$\overrightarrow{BG}•\overrightarrow{BC}$=$(\overrightarrow{BD}+\overrightarrow{DG})$•$\overrightarrow{BC}$
=$\overrightarrow{BD}•\overrightarrow{BC}$+$\overrightarrow{DG}•\overrightarrow{BC}$
=$\frac{1}{2}{\overrightarrow{BC}}^{2}$
=$\frac{1}{2}×{2}^{2}$
=2.
故答案为:2.
点评 本题考查了数量积定义及其运算性质、向量垂直与数量积的关系、等腰三角形的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
11.命题“关于x的方程的解是唯一的”的结论的否定是( )
| A. | 无解 | B. | 有两解 | ||
| C. | 至少有两解 | D. | 无解或至少有两解 |
18.下面几种推理中是演绎推理的序号为( )
| A. | 半径为r圆的面积S=πr2,则单位圆的面积S=π | |
| B. | 由金、银、铜、铁可导电,猜想:金属都可导电 | |
| C. | 由平面三角形的性质,推测空间四面体性质 | |
| D. | 由平面直角坐标系中圆的方程为(x-a)2+(y-b)2=r2,推测空间直角坐标系中球的方程为(x-a)2+(y-b)2+(z-c)2=r |
8.在△ABC中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,点D满足$\overrightarrow{BD}$+2$\overrightarrow{CD}$=$\overrightarrow{0}$,则$\overrightarrow{AD}$=( )
| A. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | B. | -$\frac{2}{3}$$\overrightarrow{a}$+$\frac{5}{3}$$\overrightarrow{b}$ | C. | $\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$ | D. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ |
15.复数$\frac{2i}{1+i}$=( )
| A. | 1+i | B. | -1+i | C. | 1-i | D. | -1-i |