题目内容
13.把长度AB和宽AD分别为2$\sqrt{3}$和2的长方形ABCD沿对角线AC折成60°的二面角,则|$\overrightarrow{BD}$|等于$\sqrt{7}$.分析 过D作DE⊥AC于E,过B作BF⊥AC于F,作EG∥FB,EG=FB,求出DG,即可求出DB.
解答  解:过D作DE⊥AC于E,过B作BF⊥AC于F,作EG∥FB,EG=FB,
解:过D作DE⊥AC于E,过B作BF⊥AC于F,作EG∥FB,EG=FB,
∴EG⊥AC,
∴∠DEG是二面角D-AC-B的平面角,
∵二面角D-AC-B为60°
∴∠DEG=60°
又AB=2$\sqrt{3}$,AD=2,
∴DE=BF=EG=$\sqrt{3}$,AE=FC=1,AC=4,EF=GB=2,EFBG是矩形
∴DG2=DE2+EG2-2DE•EGcos60°=3,
∴DB2=DG2+GB2=3+4=7,
∴DB=$\sqrt{7}$.
故答案为:$\sqrt{7}$.
点评 本题考查二面角的平面角,考查余弦定理的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
8.已知中心在原点,焦点在坐标轴上的双曲线与圆x2+y2=17有公共点A(1,-4),且圆在A点的切线与双曲线的渐近线平行,则双曲线的离心率为( )
| A. | $\frac{\sqrt{17}}{4}$ | B. | $\sqrt{17}$ | C. | $\frac{\sqrt{17}}{4}$或$\sqrt{17}$ | D. | 以上都不对 |
18.设点P(x,y),则“x=2且y=-1”是“点P在圆(x-2)2+y2=1上”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
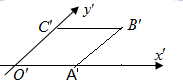 已知用斜二测画法得到四边形OABC的直观图是边长为2的菱形O′A′B′C′,如图所示,则四边形OABC的面积是( )
已知用斜二测画法得到四边形OABC的直观图是边长为2的菱形O′A′B′C′,如图所示,则四边形OABC的面积是( )