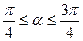题目内容
已知椭圆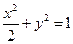 的右准线
的右准线 与
与 轴相交于点
轴相交于点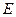 ,过椭圆右焦点
,过椭圆右焦点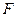 的直线与椭圆相交于
的直线与椭圆相交于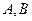 两点,点
两点,点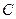 在右准线上,且
在右准线上,且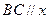 轴。
轴。
求证:直线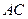 经过线段
经过线段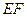 的中点。
的中点。
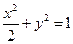 的右准线
的右准线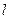 与
与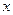 轴相交于点
轴相交于点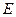 ,过椭圆右焦点
,过椭圆右焦点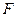 的直线与椭圆相交于
的直线与椭圆相交于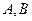 两点,点
两点,点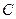 在右准线上,且
在右准线上,且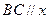 轴。
轴。求证:直线
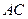 经过线段
经过线段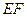 的中点。
的中点。由题设,椭圆的半焦距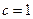 ,由焦点
,由焦点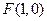 ,右准线方程为
,右准线方程为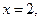 点
点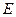 的坐标为
的坐标为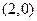 ,
,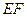 的中点为
的中点为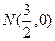 。
。
若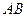 垂直于
垂直于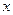 轴,则
轴,则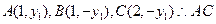 中点为
中点为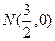 ,即
,即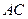 过
过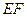 中点
中点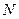 。
。
若直线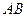 不垂直于
不垂直于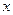 轴,由直线
轴,由直线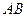 过点
过点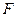 ,且由
,且由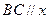 轴知点
轴知点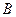 不在
不在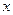 轴上,故直线
轴上,故直线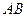 的方程为
的方程为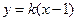 ,
,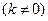
记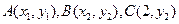 ,且
,且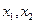 满足二次方程
满足二次方程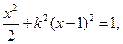 即
即
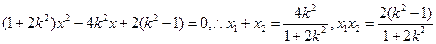
又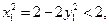 得
得
故直线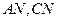 的斜率分别是
的斜率分别是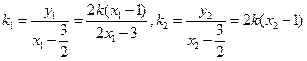
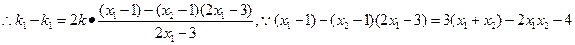
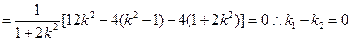
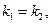 故
故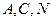 三点共线,所以,直线
三点共线,所以,直线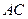 经过线段
经过线段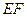 的中点
的中点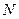
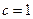 ,由焦点
,由焦点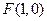 ,右准线方程为
,右准线方程为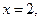 点
点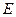 的坐标为
的坐标为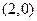 ,
,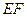 的中点为
的中点为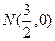 。
。若
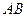 垂直于
垂直于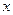 轴,则
轴,则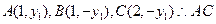 中点为
中点为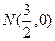 ,即
,即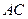 过
过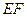 中点
中点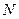 。
。若直线
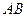 不垂直于
不垂直于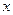 轴,由直线
轴,由直线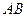 过点
过点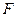 ,且由
,且由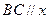 轴知点
轴知点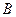 不在
不在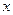 轴上,故直线
轴上,故直线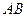 的方程为
的方程为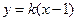 ,
,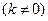
记
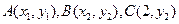 ,且
,且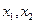 满足二次方程
满足二次方程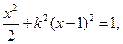 即
即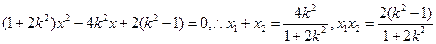
又
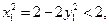 得
得
故直线
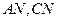 的斜率分别是
的斜率分别是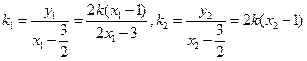
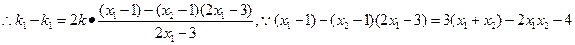
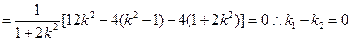
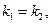 故
故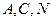 三点共线,所以,直线
三点共线,所以,直线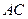 经过线段
经过线段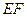 的中点
的中点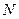
同答案

练习册系列答案
相关题目
 (
(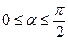 )方向行走一段时间后,再向正北方向行走一段时间,但何时改变方向不定。假定机器人行走速度为10米/分钟,则机器人行走2分钟时的可能落点区域的面积是 。
)方向行走一段时间后,再向正北方向行走一段时间,但何时改变方向不定。假定机器人行走速度为10米/分钟,则机器人行走2分钟时的可能落点区域的面积是 。
 长轴上的一个顶点为
长轴上的一个顶点为 ,以
,以 。
。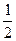 ,焦点是(-3,0),(3,0),则椭圆方程为 ( )
,焦点是(-3,0),(3,0),则椭圆方程为 ( )
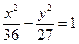


 满足
满足 ,求
,求 的最大值与最小值
的最大值与最小值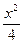 +y2=1的两焦点,P在椭圆上,当△F1PF2面积为1时,
+y2=1的两焦点,P在椭圆上,当△F1PF2面积为1时,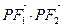 的值为
的值为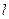 与曲线C:
与曲线C: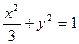 相交,若直线
相交,若直线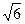 ,则直线
,则直线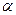 的取值范围是 ( )
的取值范围是 ( )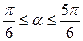 B
B 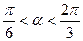 C
C 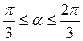 D.
D.