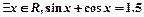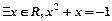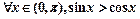题目内容
(本小题满分12分)
已知函数f(x)=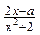 (x∈R).
(x∈R).
⑴当f(1)=1时,求函数f(x)的单调区间;
⑵设关于x的方程f(x)=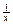 的两个实根为x1,x2,且-1≤a≤1,求|x1-x2|的最大值;
的两个实根为x1,x2,且-1≤a≤1,求|x1-x2|的最大值;
⑶在(2)的条件下,若对于[-1,1]上的任意实数t,不等式m2+tm+1≥|x1-x2|恒成立,求实数m的取值范围.
已知函数f(x)=
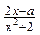 (x∈R).
(x∈R).⑴当f(1)=1时,求函数f(x)的单调区间;
⑵设关于x的方程f(x)=
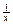 的两个实根为x1,x2,且-1≤a≤1,求|x1-x2|的最大值;
的两个实根为x1,x2,且-1≤a≤1,求|x1-x2|的最大值;⑶在(2)的条件下,若对于[-1,1]上的任意实数t,不等式m2+tm+1≥|x1-x2|恒成立,求实数m的取值范围.
(1)f(x)的减区间是(-∞,-2]和[1,+∞),增区间是[-2,1];(2)3;(3)m≥2或m≤-2
⑴由f(1)=1得a="-1" ,……………………………………………………2分
f′(x)=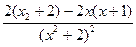 =
=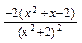 =
=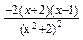 ≥0……………………4分
≥0……………………4分
-2≤x≤1,所以f(x)的减区间是(-∞,-2]和[1,+∞),增区间是[-2,1]…5分
⑵方程f(x)=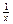 可化为x2-ax-2=0,Δ=a2+8 >0
可化为x2-ax-2=0,Δ=a2+8 >0
∴x2-ax-2=0有两不同的实根x1,x2,
则x1+x2=a,x1x2=-2…………………………7分
∴|x1-x2|=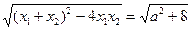
∵-1≤a≤1 ,∴当a=±1时,
∴|x1-x2|max=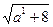 =3…………………………8分
=3…………………………8分
⑶若不等式m2+tm+1≥|x1-x2|恒成立,
由⑵可得m2+tm+1≥3,对t∈[-1,1]都成立m2+tm-2≥0 ,t∈[-1,1],
设g(t)=m2+tm-2…………………………………………9分
若使t ∈[-1,1]时g(t)≥0都成立,
则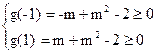 …………11分
…………11分
解得:m≥2或m≤-2 ,所以m的取值范围是m≥2或m≤-2……………………12分
f′(x)=
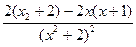 =
=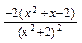 =
=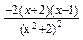 ≥0……………………4分
≥0……………………4分-2≤x≤1,所以f(x)的减区间是(-∞,-2]和[1,+∞),增区间是[-2,1]…5分
⑵方程f(x)=
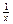 可化为x2-ax-2=0,Δ=a2+8 >0
可化为x2-ax-2=0,Δ=a2+8 >0∴x2-ax-2=0有两不同的实根x1,x2,
则x1+x2=a,x1x2=-2…………………………7分
∴|x1-x2|=
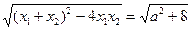
∵-1≤a≤1 ,∴当a=±1时,
∴|x1-x2|max=
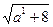 =3…………………………8分
=3…………………………8分⑶若不等式m2+tm+1≥|x1-x2|恒成立,
由⑵可得m2+tm+1≥3,对t∈[-1,1]都成立m2+tm-2≥0 ,t∈[-1,1],
设g(t)=m2+tm-2…………………………………………9分
若使t ∈[-1,1]时g(t)≥0都成立,
则
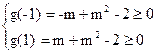 …………11分
…………11分解得:m≥2或m≤-2 ,所以m的取值范围是m≥2或m≤-2……………………12分

练习册系列答案
相关题目
 是定义在D上的函数,若对任何实数
是定义在D上的函数,若对任何实数 以及D中的任意两数
以及D中的任意两数 ,恒有
,恒有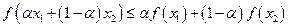 ,则称
,则称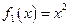 ,
,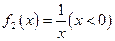 中哪些是各自定义域上的C函数,并说明理由;
中哪些是各自定义域上的C函数,并说明理由;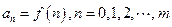 ,且
,且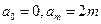 ,记
,记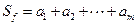 . 对于满足条件的任意函数
. 对于满足条件的任意函数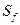 的最大值;
的最大值; ,其中,
,其中, 为实常数且
为实常数且
 的单调增区间;
的单调增区间; 对任意
对任意 恒成立,求实数
恒成立,求实数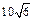 米(如图所示),旗杆底部与第一排在一个水平面上。若国歌长度约为50秒,问:升旗手应以多大的速度(米/秒)匀速升旗?
米(如图所示),旗杆底部与第一排在一个水平面上。若国歌长度约为50秒,问:升旗手应以多大的速度(米/秒)匀速升旗?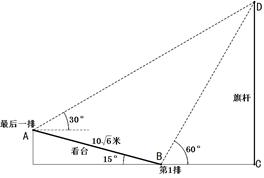
 ,则a的取值范围是 ( )
,则a的取值范围是 ( )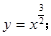 ②
②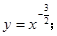 ③
③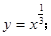 ④
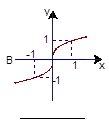
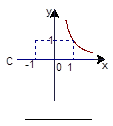
④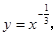 如图所示为一组函数图象,请把图象对应的解析式的号码填在相应图象下面的横线上.
如图所示为一组函数图象,请把图象对应的解析式的号码填在相应图象下面的横线上.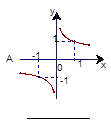

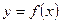 是最小正周期为2的函数,当
是最小正周期为2的函数,当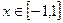 时,
时,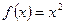 ,则函数
,则函数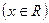 图像与
图像与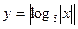 图像的交点的个数是( )
图像的交点的个数是( ) 自然数
自然数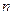
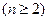 的正整数次幂,可以如下分解为
的正整数次幂,可以如下分解为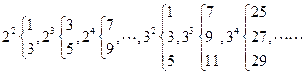
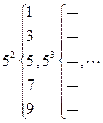
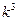
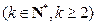 的分解中的最大数为 .
的分解中的最大数为 .