题目内容
点A、B分别是以双曲线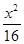
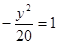 的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,
的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,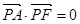
(1)求椭圆C的的方程;
(2)求点P的坐标;
(3)设M是椭圆长轴AB上的一点,点M到直线AP的距离等于|MB|,求椭圆上的点到M的距离d的最小值。
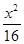
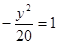 的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,
的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,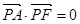
(1)求椭圆C的的方程;
(2)求点P的坐标;
(3)设M是椭圆长轴AB上的一点,点M到直线AP的距离等于|MB|,求椭圆上的点到M的距离d的最小值。
(1)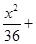
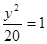 ;(2)点P的坐标为
;(2)点P的坐标为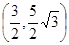 ;
;
(3)当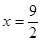 时,d取最小值
时,d取最小值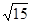 。
。
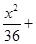
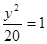 ;(2)点P的坐标为
;(2)点P的坐标为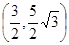 ;
;(3)当
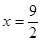 时,d取最小值
时,d取最小值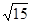 。
。试题分析:(I)求出双曲线
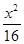
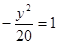 的焦点、顶点,得出椭圆的a,c,b即可求出椭圆标准方程.
的焦点、顶点,得出椭圆的a,c,b即可求出椭圆标准方程.(Ⅱ)点P的坐标为(x,y),由已知得
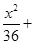
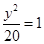 ,与(x+6)(x-4)+y2=0
,与(x+6)(x-4)+y2=0解方程组可得点P的坐标
(Ⅲ)设点M是(m,0)于是
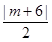 =|m-6|,解出m=2,建立椭圆上的点到M的距离d的表达式,用函数知识求最值。
=|m-6|,解出m=2,建立椭圆上的点到M的距离d的表达式,用函数知识求最值。(1)已知双曲线实半轴a1=4,虚半轴b1=2
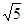 ,半焦距c1=
,半焦距c1=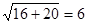 ,
,∴椭圆的长半轴a2=c1=6,椭圆的半焦距c2=a1=4,椭圆的短半轴
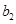 =
=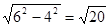 ,
,∴所求的椭圆方程为
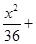
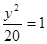 …………4分
…………4分(2)由已知
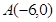 ,
,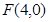 ,设点P的坐标为
,设点P的坐标为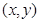 ,则
,则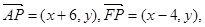 由已知得
由已知得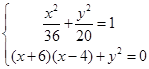 …………6分
…………6分则
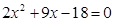 ,解之得
,解之得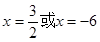 ,
, 由于y>0,所以只能取
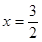 ,于是
,于是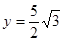 ,所以点P的坐标为
,所以点P的坐标为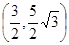 ……8分
……8分(3)直线
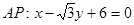 ,设点M是
,设点M是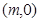 ,则点M到直线AP的距离是
,则点M到直线AP的距离是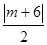 ,于是
,于是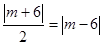 ,
,又∵点M在椭圆的长轴上,即
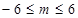
 …………10分
…………10分∴当
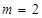 时,椭圆上的点到
时,椭圆上的点到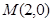 的距离
的距离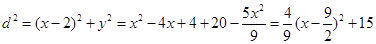
又
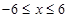 ∴当
∴当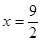 时,d取最小值
时,d取最小值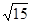 …………12分
…………12分点评:解决该试题的关键是熟练的运用双曲线的性质来表示出椭圆的a,b,c,进而得到方程,同时联立方程组,结合韦达定理求点的坐标,进而分析最值。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
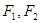 是双曲线
是双曲线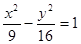 的两个焦点,点
的两个焦点,点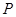 在双曲线上,且
在双曲线上,且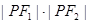
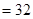 ,求证:
,求证:
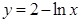 上任意一点,则点P到直线
上任意一点,则点P到直线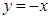 的最小距离是( )
的最小距离是( )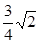
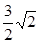
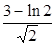
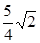
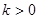 ,则方程
,则方程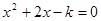 有实根;
有实根;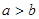 ,则
,则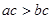 ”的否命题;
”的否命题;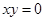 ,则
,则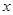 、
、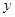 至少有一个为零”的逆否命题 .
至少有一个为零”的逆否命题 .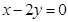 ,若双曲线经过点
,若双曲线经过点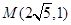 ,求此双曲线的标准方程。
,求此双曲线的标准方程。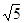 ,离心率为
,离心率为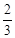 的椭圆的两个焦点分别为F1,F2,过F1作直线交椭圆于A,B两点,则△ABF2的周长为
的椭圆的两个焦点分别为F1,F2,过F1作直线交椭圆于A,B两点,则△ABF2的周长为 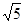 ,离心率
,离心率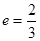 的椭圆两焦点为
的椭圆两焦点为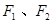 , 过
, 过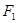 作直线交椭圆于
作直线交椭圆于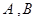 两
两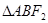 的周长为( )
的周长为( ) 
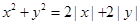 围成的图形的面积为_______________。翰林汇
围成的图形的面积为_______________。翰林汇 成等比数列,且抛物线
成等比数列,且抛物线 的顶点是
的顶点是 ,
, 等于
等于