题目内容
6.直线x-y-4=0上有一点P,它与两定点A(1,1)、B(2,3)的距离相等,则点P的坐标是($\frac{9}{2},\frac{1}{2}$).分析 设P(a,b),则a=b+4,然后由PA=PB可得$\sqrt{(a-1)^{2}+(b-1)^{2}}=\sqrt{(a-2)^{2}+(b-3)^{2}}$,联立方程可求a,b
解答 解:设P(a,b),则a=b+4①
∵PA=PB
∴$\sqrt{(a-1)^{2}+(b-1)^{2}}=\sqrt{(a-2)^{2}+(b-3)^{2}}$
整理可得,2a+4b=11②
联立①②可得,a=$\frac{9}{2},b=\frac{1}{2}$
∴P($\frac{9}{2},\frac{1}{2}$)
故答案为:P($\frac{9}{2},\frac{1}{2}$)
点评 本题主要了两点间的距离公式的应用,属于基础试题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.已知椭圆C1与抛物线C2的焦点均在x轴上,C1的中心和C2的顶点为原点O,从椭圆C1上取两个点,从椭圆C2上取一个点,将其坐标记录于表中:
(1)试判断两个点在C1上,并求出C1,C2的标准方程;
(2)已知直线l:x=my+1与椭圆C2相交于不同两点M,N,且满足$\overrightarrow{OM}⊥\overrightarrow{ON}$,求参数m的值.
| x | $\sqrt{2}$ | 2 | 4 |
| y | $\frac{\sqrt{2}}{2}$ | 0 | 4 |
(2)已知直线l:x=my+1与椭圆C2相交于不同两点M,N,且满足$\overrightarrow{OM}⊥\overrightarrow{ON}$,求参数m的值.
1.若(x-2)n展开式中共有12项,则n=( )
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
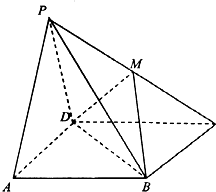 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA=PD=4,底面ABCD是边长为4的正方形,若M为PC的中点.
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA=PD=4,底面ABCD是边长为4的正方形,若M为PC的中点.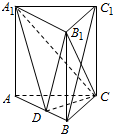 已知三棱柱ABC-A1B1C1中,侧棱垂直于底面,AC=BC,点D是AB的中点.求证:
已知三棱柱ABC-A1B1C1中,侧棱垂直于底面,AC=BC,点D是AB的中点.求证: