题目内容
1.已知a∈R,则“a>2”是“a2>2a”的充分不必要条件(填:充分不必要、必要不充分、充要、既不充分又不必要)分析 求解a2>2a,得出a>2或a<0,根据充分必要的定义判断即可得出答案.
解答 解:∵a2>2a,
∴a>2或a<0,
根据充分必要的定义判断:“a>2”是“a2>2a”的充分不必要条件,
故答案为:充分不必要.
点评 本题考查了充分必要条件的定义,属于容易题,难度不大,紧扣定义即可.

练习册系列答案
相关题目
11.已知平面向量$\overrightarrow{a},\overrightarrow{b}$满足|$\overrightarrow{a}$|=$\sqrt{2}$,$\overrightarrow{b}$=(1,0)且$\overrightarrow{a}$⊥($\overrightarrow{a}$-2$\overrightarrow{b}$),则|2$\overrightarrow{a}$+$\overrightarrow{b}$|的值为( )
| A. | $\sqrt{13}$ | B. | 13 | C. | $\sqrt{5}$ | D. | 5 |
9.已知$\overrightarrow{a}$=(4,3),$\overrightarrow{b}$=(-2,1),如果$λ\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{b}$垂直,则|$\overrightarrow{a}$-λ$\overrightarrow{b}$|的值为( )
| A. | 1 | B. | $\sqrt{5}$ | C. | 5 | D. | 2$\sqrt{5}$ |
10.已知变量x,y满足不等式组$\left\{\begin{array}{l}x+2y-1≥0\\ 2x+y-2≤0\\ x-y+2≥0\end{array}$.,则Z=8x•2y的最小值为( )
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
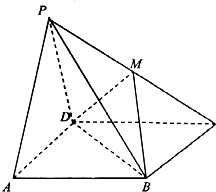 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA=PD=4,底面ABCD是边长为4的正方形,若M为PC的中点.
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA=PD=4,底面ABCD是边长为4的正方形,若M为PC的中点.