题目内容
12.已知定义域为R的函数f(x)不是偶函数,则下列命题一定为真命题的是( )| A. | ?x∈R,f(-x)≠f(x) | B. | ?x∈R,f(-x)≠-f(x) | C. | ?x0∈R,f(-x0)≠f(x0) | D. | ?x0∈R,f(-x0)≠-f(x0) |
分析 根据定义域为R的函数f(x)不是偶函数,可得:?x∈R,f(-x)=f(x)为假命题;则其否定形式为真命题,可得答案.
解答 解:∵定义域为R的函数f(x)不是偶函数,
∴?x∈R,f(-x)=f(x)为假命题;
∴?x0∈R,f(-x0)≠f(x0)为真命题,
故选:C.
点评 本题考查的知识点是函数的奇偶性的定义,全称命题的否定,难度中档.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
20.已知函数y=$\frac{{\sqrt{1-x}}}{{{x^2}-4}}$,其定义域为( )
| A. | (-∞,1] | B. | (-∞,2] | C. | (-∞,-2)∪(-2,1] | D. | [1,2)∪(2,+∞) |
17.已知集合A={1,2,3,4},B={x|x=2n,n∈A},则A∩B=( )
| A. | {1,4} | B. | {1,3} | C. | {2,4} | D. | {2,3} |
4.已知定义在R上的函数$f(x)={(\frac{1}{2})^{|x-m|}}-1$(m为实数)为偶函数,记a=f(log0.53),b=f(log25),c=f(2m),则a,b,c的大小关系为( )
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | a<c<b |
2.已知点A(-3,8),B(2,2),点P是x轴上的点,则当|AP|+|PB|最小时点P的坐标( )
| A. | (1,0) | B. | ($\frac{1}{2}$,0) | C. | ($\frac{1}{3}$,0) | D. | ($\frac{1}{4}$,0) |
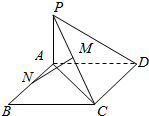 如图:ABCD为矩形,PA⊥平面ABCD,PA=AD=1,AB=2,M、N分别是PC、AB中点,请选择适当的坐标系证明:MN⊥平面PCD.
如图:ABCD为矩形,PA⊥平面ABCD,PA=AD=1,AB=2,M、N分别是PC、AB中点,请选择适当的坐标系证明:MN⊥平面PCD.