题目内容
7.已知函数f(x)=$\frac{{{x^2}+3}}{x+1}$.(1)求函数f(x)在区间[0,2]上的最值;
(2)若关于x的方程(x+1)f(x)-ax=0在区间(1,4)内有两个不等实根,求实数a的取值范围.
分析 (1)利用换元法令t=x+1,t∈[1,3],从而化为y=t+$\frac{4}{t}$-2,从而求闭区间上的最值;
(2)当x∈(1,4)时,可化方程为a=$\frac{{x}^{2}+3}{x}$=x+$\frac{3}{x}$,从而作函数y=x+$\frac{3}{x}$在(1,4)上的图象,结合图象求解即可.
解答 解:(1)令t=x+1,t∈[1,3],
则x=t-1,
故y=f(x)=$\frac{{{x^2}+3}}{x+1}$=$\frac{(t-1)^{2}+3}{t}$=t+$\frac{4}{t}$-2,
由对勾函数的性质可知,
函数y=g(t)=t+$\frac{4}{t}$-2在[1,2]上单调递减,在[2,3]上单调递增;
且g(1)=1+4-2=3,g(2)=2+2-2=2,g(3)=3+$\frac{4}{3}$-2=$\frac{7}{3}$,
故函数f(x)在区间[0,2]上的最小值为2,最大值为3;
(2)当x∈(1,4)时,
∵(x+1)f(x)-ax=0,
∴(x2+3)-ax=0,
故a=$\frac{{x}^{2}+3}{x}$=x+$\frac{3}{x}$,
作函数y=x+$\frac{3}{x}$在(1,4)上的图象如下,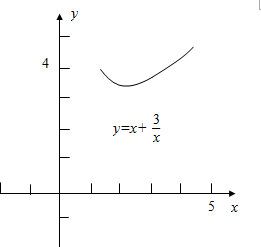 ,
,
其中ymin=$\sqrt{3}$+$\sqrt{3}$=2$\sqrt{3}$,y|x=1=1+3=4,y|x=4=4+$\frac{3}{4}$>4,
故结合图象可知,当2$\sqrt{3}$<a<4时,
关于x的方程(x+1)f(x)-ax=0在区间(1,4)内有两个不等实根.
故实数a的取值范围为2$\sqrt{3}$<a<4.
点评 本题考查了函数的最值的求法及数形结合的思想应用.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
17.函数f(x)=$\sqrt{x-1}+{log_3}(4-x)$的定义域是( )
| A. | ∅ | B. | (1,4) | C. | [1,4) | D. | (-∞,1)∪[4,+∞] |
2.设集合A={x|1≤x≤6,x∈N},对于A的每个非空子集,定义其“交替和”如下:把集合中的数按从大到小的顺序排列,然后从最大的数开始交替地加减各数(如:{1,2,5}的“交替和”是5-2+1=4,{6,3}的“交替和”就是6-3=3,{3}的“交替和”就是3).则集合A的所有这些“交替和”的总和为( )
| A. | 128 | B. | 192 | C. | 224 | D. | 256 |
12.已知定义域为R的函数f(x)不是偶函数,则下列命题一定为真命题的是( )
| A. | ?x∈R,f(-x)≠f(x) | B. | ?x∈R,f(-x)≠-f(x) | C. | ?x0∈R,f(-x0)≠f(x0) | D. | ?x0∈R,f(-x0)≠-f(x0) |
19.函数f(x)=x2+lnx的零点个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
16.在△ABC中,∠A=60°,|$\overrightarrow{AB}$|=2,|$\overrightarrow{AC}$|=1,则$\overrightarrow{AB}$•$\overrightarrow{AC}$的值为( )
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |