题目内容
【题目】如图,在直三棱柱![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,
,![]() .
.![]() 是线段
是线段![]() 的中点.
的中点.
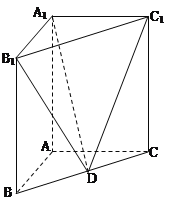
(1)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)求二面角![]() 的大小的余弦值.
的大小的余弦值.
【答案】(1)![]() (2)
(2)![]()
【解析】
试题(1)利用空间向量研究线面角,首先建立恰当空间直角坐标系,设立各点坐标,利用方程组求面![]() 的法向量,最后利用向量数量积求夹角余弦值的绝对值,也是线面角的正弦值(2)利用空间向量研究二面角,首先建立恰当空间直角坐标系,设立各点坐标,利用方程组求两个平面的法向量,最后利用向量数量积求夹角余弦值,根据图形确定二面角
的法向量,最后利用向量数量积求夹角余弦值的绝对值,也是线面角的正弦值(2)利用空间向量研究二面角,首先建立恰当空间直角坐标系,设立各点坐标,利用方程组求两个平面的法向量,最后利用向量数量积求夹角余弦值,根据图形确定二面角![]() 的大小的余弦值与夹角余弦值之间关系.
的大小的余弦值与夹角余弦值之间关系.
试题解析:因为在直三棱柱![]() 中,
中,![]() ,所以分别以
,所以分别以![]() 、
、![]() 、
、![]() 所在的直线为
所在的直线为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
则![]() ,
,
因为![]() 是
是![]() 的中点,所以
的中点,所以![]() ,
,
(1)因为![]() ,设平面
,设平面![]() 的法向量
的法向量![]() ,
,
则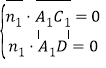 ,即
,即![]() ,取
,取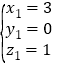 ,
,
所以平面![]() 的法向量
的法向量![]() ,而
,而![]() ,
,
所以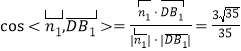 ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ;
;
(2)![]() ,
,![]() ,设平面
,设平面![]() 的法向量
的法向量![]() ,
,
则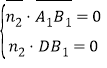 ,即
,即![]() ,取
,取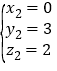 ,平面
,平面![]() 的法向量
的法向量![]() ,
,
所以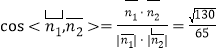 ,
,
二面角![]() 的大小的余弦值
的大小的余弦值![]() .
.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
