Question

【题目】已知某个机械零件是由两个有公共底面的圆锥组成的，且这两个圆锥有公共点的母线互相垂直，把这个机械零件打磨成球形，该球的半径最大为1，设这两个圆锥的高分别为，则的最小值为__________．

Answer 1

【答案】

【解析】

根据题意作出轴截面的示意图，由等面积法得出两圆锥的母线的长度关系，再运用均值不等式和勾股定理可得出的最小值．

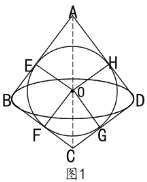
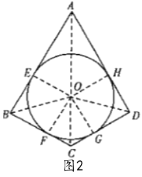
由题意可知,打磨后所得半径最大的球是由这两个圆锥构成的组合体的内切球,如图1所示，内切球的半径R =1,如图2为这个组合体的轴截面示意图，圆0为内切球的轴截面，E,F,G,H分别为切点,连接，由题意可知，

则四边形ABCD的面积为，

即，

所以

由基本不等式可得，则，当且仅当时等号成立，

所以，当且仅当时等号成立，

所以的最小值为，

故填：。