题目内容
【题目】已知函数f(x)=axlnx﹣x2﹣ax+1(a∈R)在定义域内有两个不同的极值点.
(1)求实数a的取值范围;
(2)设两个极值点分别为x1,x2,x1<x2,证明:f(x1)+f(x2)<2﹣x12+x22.
【答案】(1)a>2e(2)证明见解析
【解析】
(1)先对函数求导,然后结合导数与单调性的关系对a进行分类讨论,确定导数正负即可求解函数单调性,结合单调性即可求解;
(2)分析要证明不等式特点,进行合理的变形,然后构造函数,结合导数及函数性质可证.
(1)由题意可知,f(x)的定义域为(0,+∞),f'(x)=alnx﹣2x,
令g(x)=alnx﹣2x(x>0),
由函数f(x)在定义域内有两个不同的极值点,可知g(x)在区间(0,+∞)内有两个不同的变号零点,
由![]() 可知,
可知,
当a≤0时,g'(x)<0恒成立,即函数g(x)在(0,+∞)上单调,不符合题意,舍去.
当a>0时,由g'(x)>0得,![]() ,即函数g(x)在区间
,即函数g(x)在区间![]() 上单调递增;
上单调递增;
由g'(x)<0得,![]() ,即函数g(x)在区间
,即函数g(x)在区间![]() 上单调递减;
上单调递减;
故要满足题意,必有![]() ,
,
解得:a>2e;
又![]() ,∴函数g(x)在(1,
,∴函数g(x)在(1,![]() )内有一个零点,
)内有一个零点,
又当![]() 时,g(x)
时,g(x)![]() ,∴在(
,∴在(![]() )内有一个零点,
)内有一个零点,
∴a>2e满足题意.
(2)由(1)可知,![]() ,
,
故要证:![]() ,
,
只需证明:![]() ,
,
即证: 不妨设0<x1<x2,即证
不妨设0<x1<x2,即证![]() ,
,
构造函数:h(t)=lnt﹣t2+1(t>1)其中![]() ,
,
由![]() ,所以函数h(t)在区间(1,+∞)内单调递减,所以h(t)<h(1)=0得证.
,所以函数h(t)在区间(1,+∞)内单调递减,所以h(t)<h(1)=0得证.

【题目】在贯彻中共中央国务院关于精准扶贫政策的过程中,某单位定点帮扶100户贫困户.工作组对这100户村民的贫困状况和家庭成员受教育情况进行了调查:甲村55户贫困村民中,家庭成员接受过中等及以上教育的只有10户,乙村45户贫困村民中,家庭成员接受过中等及以上教育的有20户.
(1)完成下面的列联表,并判断是否有99.5%的把握认为贫困与接受教育情况有关;
家庭成员接受过中等以下 教育的户数 | 家庭成员接受过中等及以上 教育的户数 | 合计 | |
甲村贫困户数 | |||
乙村贫困户数 | |||
合计 |
(2)在被帮扶的100户贫困户中,按分层抽样的方法从家庭成员接受过中等及以上教育的贫困户中抽取6户,再从这6户中采用简单随机抽样的方法随机抽取2户,求这2户中甲、乙两村恰好各1户的概率.
参考公式与数据: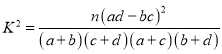 ,其中
,其中![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】为了研究某学科成绩是否与学生性别有关,采用分层抽样的方法,从高三年级抽取了30名男生和20名女生的该学科成绩,得到如下所示男生成绩的频率分布直方图和女生成绩的茎叶图,规定80分以上为优分(含80分).


(Ⅰ)(i)请根据图示,将2×2列联表补充完整;
优分 | 非优分 | 总计 | |
男生 | |||
女生 | |||
总计 | 50 |
(ii)据此列联表判断,能否在犯错误概率不超过10%的前提下认为“该学科成绩与性别有关”?
(Ⅱ)将频率视作概率,从高三年级该学科成绩中任意抽取3名学生的成绩,求至少2名学生的成绩为优分的概率.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() .
.
【题目】近五年来某草场羊只数量与草场植被指数两变量间的关系如表所示,绘制相应的散点图,如图所示:
年份 | 1 | 2 | 3 | 4 | 5 |
羊只数量(万只) | 1.4 | 0.9 | 0.75 | 0.6 | 0.3 |
草地植被指数 | 1.1 | 4.3 | 15.6 | 31.3 | 49.7 |

根据表及图得到以下判断:①羊只数量与草场植被指数成减函数关系;②若利用这五组数据得到的两变量间的相关系数为![]() ,去掉第一年数据后得到的相关系数为
,去掉第一年数据后得到的相关系数为![]() ,则
,则![]() ;③可以利用回归直线方程,准确地得到当羊只数量为2万只时的草场植被指数;以上判断中正确的个数是( )
;③可以利用回归直线方程,准确地得到当羊只数量为2万只时的草场植被指数;以上判断中正确的个数是( )
A.0B.1C.2D.3
