Question

【题目】已知函数f（x）＝|x﹣1|+|2x+2|，g（x）＝|x+2|﹣|x﹣2a|+a.

（1）求不等式f（x）＞4的解集；

（2）对x1∈R，x2∈R，使得f（x1）≥g（x2）成立，求a的取值范围.

Answer 1

【答案】（1）（2）[﹣4，0]

【解析】

（1）根据绝对值的几何意义，去掉绝对值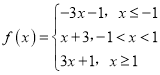，再分类解不等式f（x）＞4.

（2）根据对x1∈R，x2∈R，使得f（x1）≥g（x2）成立，则f（x）min≥g（x）min，由（1）知， f（x）min＝2，g（x）＝|x+2|+|x﹣2a|+a≥|（x+2）﹣（x﹣2a）|+a＝|2a+2|+a，解不等式2≥|2a+2|+a即可.

（1）因为，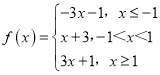

所以f（x）＞4即为或或，

解得或x＞1，

所以不等式的解集为；

（2）由（1）知，当x＝﹣1时，f（x）min＝2，g（x）＝|x+2|+|x﹣2a|+a≥|（x+2）﹣（x﹣2a）|+a＝|2a+2|+a，

由题意，对x1∈R，x2∈R，使得f（x1）≥g（x2）成立，

故f（x）min≥g（x）min，

即2≥|2a+2|+a，

所以

解得﹣4≤a≤0，

所以实数a的取值范围为[﹣4，0].