��Ŀ����
����Ŀ�������жϣ�
�ٴӸ�����Ϊ1��2������1000�������г�ȡһ������Ϊ50��������������ϵͳ�����������г�ȡ����ֶμ��ӦΪ20��
����֪ij�ֲ�Ʊ���н�����Ϊ ![]() ����ô��1000�����ֲ�Ʊ��һ�����н�������ò�Ʊ���㹻����������
����ô��1000�����ֲ�Ʊ��һ�����н�������ò�Ʊ���㹻����������
�۴�װ��2�������2���\��Ŀڴ�����ȡ2����ǡ��1���\����ǡ��2���\���ǻ���������������¼���
�������������ع�ϵ�ı�����һ�������ǣ�1��3������2��5������3��6������6��8���������ǵĻع�ֱ��һ�����㣨3�� ![]() ����
����
������ȷ������ǣ� ��
A.�١��ڡ���
B.�١��ۡ���
C.�ۡ���
D.�١���
���𰸡�B
���������⣺�ٴӸ�����Ϊ1��2������1000�������г�ȡһ������Ϊ50��������������ϵͳ�����������г�ȡ����ֶμ��ӦΪ ![]() =20����ȷ��
=20����ȷ��
����֪ij�ֲ�Ʊ���н�����Ϊ ![]() ����ô��1000�����ֲ�Ʊ���ܻ��н�������ò�Ʊ���㹻��������������ȷ��
����ô��1000�����ֲ�Ʊ���ܻ��н�������ò�Ʊ���㹻��������������ȷ��
�۴�װ��2�������2���\��Ŀڴ�����ȡ2����ȡ�����������2�����Ǻ���2�����Ǻ���1������1���������࣮ǡ��1���\����ǡ��2���\�ⲻ��������ȷ��
�������������ع�ϵ�ı�����һ�������ǣ�1��3������2��5������3��6������6��8���������ǵĻع�ֱ��һ�����㣨3�� ![]() ������ȷ��
������ȷ��
��ѡ��B��
��4��ѡ��ֱ�����жϣ����ɵó����ۣ�

����Ŀ���ڡ�һ��һ·���Ľ����У���ʯ�����Ż����ij�����������Ŀ���Ȩ�������ڸõ������������̽�˼��ھ���ȡ���˵�������.����ȫ�濱̽ʱ�ں��Ű�����������þ�λ����ȫ�濱̽.���ڿ�̽һ�ھ��ķ��úܸߣ��������Ƶľ�λ��ԭ�о�λ�غϻ�ӽ��������þɾ��ĵ������ϣ����ش�����¾����Խ�Լ��̽����.��̽�������������±���
����I | 1 | 2 | 3 | 4 | 5 | 6 |
���� |
|
|
|
|
|
|
��̽��� | 2 | 4 | 5 | 6 | 8 | 10 |
������ | 40 | 70 | 110 | 90 | 160 | 205 |
��1����ɢ��ͼ��![]() �žɾ�λ�ô��·ֲ���һ��ֱ�߸���������ǰ5��������ûع��߷���Ϊ
�žɾ�λ�ô��·ֲ���һ��ֱ�߸���������ǰ5��������ûع��߷���Ϊ![]() ����
����![]() ��������
��������![]() ��Ԥ��ֵ��
��Ԥ��ֵ��
��2��������̽�¾�![]() ����ͨ��1��3��5��7�ž��������
����ͨ��1��3��5��7�ž��������![]() ��ֵ��
��ֵ��![]() ��ȷ��0.01������ڣ�1����
��ȷ��0.01������ڣ�1����![]() ��ֵ֮�����
��ֵ֮����� ![]() ��������10%����ʹ��λ����ӽ������оɾ�
��������10%����ʹ��λ����ӽ������оɾ�![]() ����������λ�ô����жϿɷ�ʹ�þɾ������ο���ʽ�ͼ�������
����������λ�ô����жϿɷ�ʹ�þɾ������ο���ʽ�ͼ������� 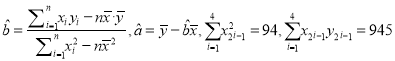 ��
��
��3�������������̽��ȵı�ֵ![]() ������20�Ŀ�̽����Ϊ���ʾ�����ԭ�о���
������20�Ŀ�̽����Ϊ���ʾ�����ԭ�о���![]() �ľ������⿱̽3�ھ�����ǡ��2�������ʾ��ĸ��ʣ�
�ľ������⿱̽3�ھ�����ǡ��2�������ʾ��ĸ��ʣ�