题目内容
设椭圆的中心为坐标原点,它在x轴上的一个焦点与短轴两端点连成60°的角,两准线间的距离等于8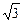 ,求椭圆方程.
,求椭圆方程.
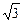 ,求椭圆方程.
,求椭圆方程.
椭圆方程为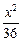 +
+ 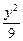 =1.
=1.
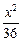 +
+ 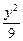 =1.
=1.依题意,设所求椭圆方程为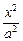 +
+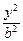 =1,
=1,
∵椭圆右焦点F(c,0)与短轴两端点A、B连成60°的角,
如图,则∠AFB=60°,△AFB为等边三角形,
于是有a=2b. ①
又由两准线间的距离等于8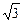 ,得
,得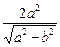 =8
=8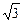 . ②
. ②
联立①②两方程,解得a=6,b=3.
故所求椭圆方程为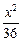 +
+ 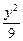 =1.
=1.
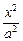 +
+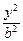 =1,
=1,∵椭圆右焦点F(c,0)与短轴两端点A、B连成60°的角,
如图,则∠AFB=60°,△AFB为等边三角形,
于是有a=2b. ①
又由两准线间的距离等于8
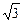 ,得
,得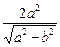 =8
=8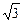 . ②
. ②联立①②两方程,解得a=6,b=3.
故所求椭圆方程为
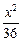 +
+ 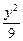 =1.
=1.
练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
 +
+ =1(a>b>0)的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点.
=1(a>b>0)的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点. ,
,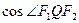 的取值范围;
的取值范围; ,试求直线PM的斜率
,试求直线PM的斜率 的范围。
的范围。 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,直线y=
,直线y= x+1与椭圆相交于A、B两点,点M在椭圆上,
x+1与椭圆相交于A、B两点,点M在椭圆上, =
= +
+ ,求椭圆的方程.
,求椭圆的方程.




 的左、右焦点, 三个内角A、B、C满足
的左、右焦点, 三个内角A、B、C满足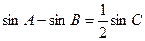 , 则顶点C的轨迹方程是( ).
, 则顶点C的轨迹方程是( ). 

 (
( >0,
>0, >0)的左焦点为F,右顶点为A,上顶点为B,若
>0)的左焦点为F,右顶点为A,上顶点为B,若


 翰林汇
翰林汇