题目内容
【题目】若函数![]() ,当
,当![]() 时,函数
时,函数![]() 有极值
有极值![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 的极值;
的极值;
(3)若关于![]() 的方程
的方程![]() 有三个不同的实数解,求实数
有三个不同的实数解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)极大值
(2)极大值![]() ,极小值
,极小值![]() ,(3)
,(3)![]()
【解析】
(1)求导,根据极值的定义得到![]() ,代入数据解得答案.
,代入数据解得答案.
(2)求导得到单调区间,计算极值得到答案.
(3)变换得到![]() 有三个交点,画出函数图像,根据图像得到答案.
有三个交点,画出函数图像,根据图像得到答案.
(1)函数![]() ,
,![]() ,
,
由题意知,当![]() 时,函数
时,函数![]() 有极值
有极值![]() ,
,![]() ,
,
即![]() ,解得
,解得![]() ,故所求函数的解析式为
,故所求函数的解析式为![]() ;
;
(2)由(1)得![]() ,令
,令![]() ,得
,得![]() 或
或![]() ,
,
当![]() 变化时,
变化时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
| 单调递增 |
| 单调递减 |
| 单调递增 |
因此,当![]() 时,
时,![]() 有极大值2,当
有极大值2,当![]() 时,
时,![]() 有极小值-2,
有极小值-2,
(3)画出函数图像,如图所示:
要使方程![]() 有三个不同的实数解,即
有三个不同的实数解,即![]() 有三个交点,
有三个交点,
根据图像知:![]() .
.
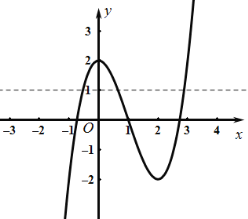

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
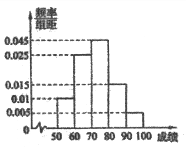
【题目】某校高三年级共有学生![]() 名,为了解学生某次月考的情况,抽取了部分学生的成绩(得分均为整数,满分为
名,为了解学生某次月考的情况,抽取了部分学生的成绩(得分均为整数,满分为![]() 分)进行统计,绘制出如下尚未完成的频率分布表:
分)进行统计,绘制出如下尚未完成的频率分布表:
分组 | 频数 | 频率 |
|
|
|
|
| |
|
| |
|
| |
| ||
|
|
(1)补充完整题中的频率分布表;
(2)若成绩在![]() 为优秀,估计该校高三年级学生在这次月考中,成绩优秀的学生约为多少人.
为优秀,估计该校高三年级学生在这次月考中,成绩优秀的学生约为多少人.