题目内容
【题目】在棱长均为![]() 的四面体
的四面体![]() 中,点
中,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 的中点.若点
的中点.若点![]() ,
,![]() 是平面
是平面![]() 内的两动点,且
内的两动点,且![]() ,
,![]() ,则
,则![]() 的面积为( )
的面积为( )
A. ![]() B. 3
B. 3
C. ![]() D. 2
D. 2
【答案】C
【解析】
建立空间直角坐标系,写出B,E,F的坐标,设M(x,y,0)的坐标,由![]() ,得出M的轨迹,同理得出N的轨迹,由
,得出M的轨迹,同理得出N的轨迹,由![]() ,即可得到
,即可得到![]() 的面积.
的面积.
建立空间直角坐标系如图所示,
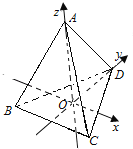
![]() ,底面
,底面![]() 为等边三角形,且
为等边三角形,且![]() .所以OD=2,B(-
.所以OD=2,B(-![]() ,-1,0),D(0,2,0),C(
,-1,0),D(0,2,0),C(![]() ,-1,0),点
,-1,0),点![]() 为
为![]() 的中点,所以E(
的中点,所以E(![]() ,
,![]() ,0),点
,0),点![]() 为
为![]() 的中点,F(-
的中点,F(-![]() ,-
,-![]() ,0),设M(x,y,0),
,0),设M(x,y,0),![]() ,
,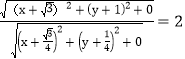 ,化简得
,化简得![]() ,且点M 是平面BCD 内的动点,所以点M在以(0,0)为圆心,以1为半径的圆上,又
,且点M 是平面BCD 内的动点,所以点M在以(0,0)为圆心,以1为半径的圆上,又![]() ,且点N 是平面BCD 内的动点,同理N也在这个圆上,且
,且点N 是平面BCD 内的动点,同理N也在这个圆上,且![]() ,所以MN为圆的直径,因为AO
,所以MN为圆的直径,因为AO![]() 面BCD,所以AO
面BCD,所以AO![]() MN,且AO=
MN,且AO=![]() ,
,![]() .
.
故选:C.

【题目】“中国大能手”是央视推出的一档大型职业技能挑战赛类节目,旨在通过该节目,在全社会传播和弘扬“劳动光荣、技能宝贵、创造伟大”的时代风尚.某公司准备派出选手代表公司参加“中国大能手”职业技能挑战赛.经过层层选拔,最后集中在甲、乙两位选手在一项关键技能的区分上,选手完成该项挑战的时间越少越好.已知这两位选手在15次挑战训练中,完成该项关键技能挑战所用的时间![]() (单位:秒)及挑战失败(用“×”表示)的情况如下表1:
(单位:秒)及挑战失败(用“×”表示)的情况如下表1:
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| × | 96 | 93 | × | 92 | × | 90 | 86 | × | × | 83 | 80 | 78 | 77 | 75 |
| × | 95 | × | 93 | × | 92 | × | 88 | 83 | × | 82 | 80 | 80 | 74 | 73 |
据上表中的数据,应用统计软件得下表2:
均值(单位:秒)方差 | 方差 | 线性回归方程 | |
甲 | 85 | 50.2 |
|
乙 | 84 | 54 |
|
(1)根据上述回归方程,预测甲、乙分别在下一次完成该项关键技能挑战所用的时间;
(2)若该公司只有一个参赛名额,根据以上信息,判断哪位选手代表公司参加职业技能挑战赛更合适?请说明你的理由.
