题目内容
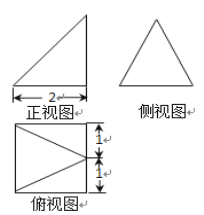
【题目】一个几何体的三视图如图所示，若该几何体的外接球表面积为
，则该几何体的体积为( )
A. 
B. 
C. 
D. 
【答案】B
【解析】
先将几何体还原得四棱锥P-ABCD，做底面中心的垂线，通过列方程找到球心的位置，进而再求四棱锥的高，从而可得体积.
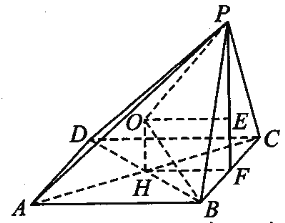
由三视图可知该几何体为四棱锥P-ABCD，其中ABCD是边长为2的正方形，侧面PBC垂直于底面ABCD，
为等腰三角形.
设BC的中点为F，四边形ABCD的中心为点H，连接PF,FH，过点H作平面ABCD的垂线，则球心在该直线上，即为点O，过点O作
于点E，连接OP.
设四棱锥P-ABCD的外接球半径为R，由其表面积为
，得
，解得
.
设OH=x，则在直角三角形OHB中，有
，解得
.
在直角三角形POE中，
，所以
，解得
.（负值已舍去）
所以PF=PE+EF=2.
所以四棱锥P-ABCD的体积
.
故选B.
练习册系列答案
相关题目
