题目内容
【题目】已知圆![]() 的任意一条切线l与椭圆
的任意一条切线l与椭圆![]() 都有两个不同交点A,B(O是坐标原点)
都有两个不同交点A,B(O是坐标原点)
(1)求圆O半径r的取值范围;
(2)是否存在圆O,使得![]() 恒成立?若存在,求出圆O的方程及
恒成立?若存在,求出圆O的方程及![]() 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由.
【答案】(1)![]() (2)见详解
(2)见详解
【解析】
(1)圆![]() 的中心是原点,椭圆的短半轴长为
的中心是原点,椭圆的短半轴长为![]() ,根据圆和椭圆的位置关系分析即得;(2)当圆的切线的斜率存在时,设
,根据圆和椭圆的位置关系分析即得;(2)当圆的切线的斜率存在时,设![]() ,圆的切线为
,圆的切线为![]() ,与
,与![]() 联立,可得
联立,可得![]() ,根据韦达定理和
,根据韦达定理和![]() ,可得
,可得![]() 和
和![]() 的关系式,再由圆心到切线
的关系式,再由圆心到切线![]() 的距离等于半径,可得
的距离等于半径,可得![]() ,解出
,解出![]() ,即得;当切线斜率不存在时,可得上述圆的切线,进而求出切点,验证满足
,即得;当切线斜率不存在时,可得上述圆的切线,进而求出切点,验证满足![]() 即可,故使得
即可,故使得![]() 恒成立的圆存在;当切线斜率存在且不等于
恒成立的圆存在;当切线斜率存在且不等于![]() 时,则有
时,则有![]() ,由韦达定理和基本不等式可得
,由韦达定理和基本不等式可得![]() 的最大值,当切线斜率不存在或等于
的最大值,当切线斜率不存在或等于![]() 时,可知
时,可知![]() 的值,选两者中的最大值,再由
的值,选两者中的最大值,再由![]() ,计算即得.
,计算即得.
(1)当![]() 时,圆
时,圆![]() 在椭圆内部,切点在椭圆内,圆的每一条切线都过椭圆内部的点,切线与椭圆总有两个不同交点,满足题意;当
在椭圆内部,切点在椭圆内,圆的每一条切线都过椭圆内部的点,切线与椭圆总有两个不同交点,满足题意;当![]() 时,圆的切线
时,圆的切线![]() 和
和![]() 都和椭圆最多只有一个公共点,不满足题意;
都和椭圆最多只有一个公共点,不满足题意;
故![]() 的取值范围是
的取值范围是![]() .
.
(2)当圆的切线的斜率存在时,设圆的切线为![]() ,设
,设![]() ,由
,由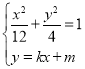 消去
消去![]() 得:
得:![]() ,则
,则![]() ,
,![]() ,则
,则![]()
![]() ,由
,由![]() 得
得![]() ,即
,即![]() ,
,![]() ,又由
,又由![]() 与圆
与圆![]() 相切得
相切得![]() ,即
,即![]() ,解得
,解得![]() ,此时圆
,此时圆![]() 的方程为
的方程为![]() .
.
当切线斜率不存在时,上述圆的切线为![]() 或
或![]() ,这两条切线与椭圆的交点为
,这两条切线与椭圆的交点为![]() ,
,![]() 或
或![]() ,
,![]() ,也满足
,也满足![]() ,故满足条件的圆
,故满足条件的圆![]() 存在,其方程为
存在,其方程为![]() .
.
当切线斜率存在且不等于![]() 时,因为
时,因为![]()
![]()
![]()
![]()
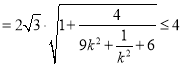 ,当且仅当
,当且仅当![]() 时取等号;
时取等号;
当切线斜率不存在或等于![]() 时,
时,![]() ,则
,则![]() ,又
,又![]() ,故
,故![]()
![]() ,则
,则![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了分析某个高三学生的学习状态,对其下一阶段的学习提供指导性建议.现对他前7次考试的数学成绩![]() 、物理成绩
、物理成绩![]() 进行分析.下面是该生7次考试的成绩.
进行分析.下面是该生7次考试的成绩.
数学 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
(1)他的数学成绩与物理成绩哪个更稳定?请给出你的证明;
(2)已知该生的物理成绩![]() 与数学成绩
与数学成绩![]() 是线性相关的,若该生的物理成绩达到115分,请你估计他的数学成绩大约是多少?并请你根据物理成绩与数学成绩的相关性,给出该生在学习数学、物理上的合理建议.
是线性相关的,若该生的物理成绩达到115分,请你估计他的数学成绩大约是多少?并请你根据物理成绩与数学成绩的相关性,给出该生在学习数学、物理上的合理建议.
参考公式:方差公式:![]() ,其中
,其中![]() 为样本平均数.
为样本平均数. ,
,![]() 。
。