Question

【题目】为美化城市环境，相关部门需对一半圆形中心广场进行改造出新，为保障市民安全，施工队对广场进行围挡施工．如图，围挡经过直径的两端点A，B及圆周上两点C，D围成一个多边形ABPQR，其中AR，RQ，QP，PB分别与半圆相切于点A，D，C，B．已知该半圆半径OA长30米，∠COD为60°，设∠BOC为．

（1）求围挡内部四边形OCQD的面积；

（2）为减少对市民出行的影响，围挡部分面积要尽可能小．求该围挡内部多边形ABPQR面积的最小值？并写出此时的值．

Answer 1

【答案】（1）（2）围挡内部多边形ABPQR面积的最小值为900平方米，此时

【解析】

（1）连接将四边形变为两个全等的直角三角形，求得的长度后可计算得面积.（2）根据（1）的方法，求得多边形的面积，求得总面积的表达式，利用换元法以及基本不等式求得多边形面积的最小值以及此时的值.

解：

（1）连接OQ，因为QD，QC为圆O的切线，所以QD＝QC，OD＝OC＝30，

OQ＝OQ，所以△ODQ≌△OCQ，所以∠DOQ＝∠COQ＝30°，

又因为OD⊥DQ，所以＝tan30°＝，所以DQ＝10，

所以S△ODQ＝OD·DQ＝150，所以SOCQD=2S△ODQ =300；

即围挡内部四边形OCQD的面积为300平方米；

（2）BP=OB tan，SOBPC=2S△OBP=900 tan，同理SOARD=2S△OAR=900 tan(－)，

SABPQR=900[tan+ tan(－)]＋300，

即求 tan+ tan(－)的最小值，

tan+ tan(－)= tan+=（*）

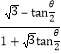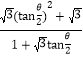令，由得x(1，4)

则（*）=≥，当且仅当x=2时取等号，此时，

故Smin=900×+300=900，

答：围挡内部多边形ABPQR面积的最小值为900平方米，此时